Question

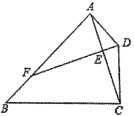
【题目】如图，在正方形ABCD中，H是对角线BD的中点，延长DC至E，使得DE=DB，连接BE，作DF⊥BE交BC于点G，交BE于点F，连接CH、FH，下列结论：（1）HC=HF；（2）DG=2EF；（3）BE·DF=2CD2；（4）S△BDE=4S△DFH；（5）HF∥DE，正确的个数是（ ）

A.5B.4C.3D.2

Answer 1

【答案】B

【解析】

由等腰三角形“三线合一”的性质可得EF=BF，根据H是正方形对角线BD的中点可得CH=DH=BH，即可证明HF是△BDE的中位线，可得HF=DE，HF//DE；由BD=DE即可得HC=HF；利用直角三角形两锐角互余的关系可得∠CBE=∠CDG，利用ASA可证明△BCE≌△DCG，可得DG=BE，可判定DG=2EF，由正方形的性质可得BD2=2CD2，根据∠CBE=∠CDG，∠E是公共角可证明△BCE∽△DFE，即可得，即BE·DF=DE·BC，可对③进行判定，根据等底等高的三角形面积相等可对④进行判定，综上即可得答案.

∵BD=DE，DF⊥BE，

∴EF=BF，

∵H是正方形ABCD对角线BD的中点，

∴CH=DH=BH=BD，

∴HF是△BDE的中位线，

∴HF=DE=BD=CH，HF//DE，故①⑤正确，

∵∠CBE+∠E=90°，∠FDE+∠E=90°，

∴∠CBE=∠FDE，

又∵CD=BC，∠DCG=∠BCE=90°，

∴△BCE≌△DCG，

∴DG=BE，

∵BE=2EF，

∴DG=2EF，故②正确，

∵∠CBE=∠FDE，∠E=∠E，

∴△BCE∽△DFE，

∴，即BE·DF=DE·BC，

∵BD2=CD2+BC2=2CD2

∴DE2=2CD2，

∴DE·BC≠2CD2，

∴BE·DF≠2CD2，故③错误，

∵DH=BD，

∴S△DFH=S△DFB，

∵BF=BE，

∴S△DFB=S△BDE，

∴S△DFH=S△BDE，即S△BDE=4S△DFH，故④正确，

综上所述：正确的结论有①②④⑤，共4个，

故选B.