Question

【题目】把函数C1：y＝ax2﹣2ax﹣3a（a≠0）的图象绕点P（m，0）旋转180°，得到新函数C2的图象，我们称C2是C1关于点P的相关函数．C2的图象的对称轴与x轴交点坐标为（t，0）．

（1）填空：t的值为　 　（用含m的代数式表示）

（2）若a＝﹣1，当≤x≤t时，函数C1的最大值为y1，最小值为y2，且y1﹣y2＝1，求C2的解析式；

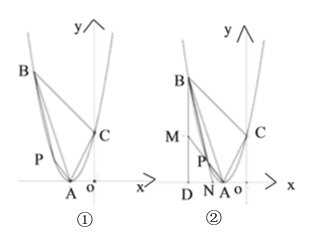
（3）当m＝0时，C2的图象与x轴相交于A，B两点（点A在点B的右侧）．与y轴相交于点D．把线段AD原点O逆时针旋转90°，得到它的对应线段A′D′，若线A′D′与C2的图象有公共点，结合函数图象，求a的取值范围．

Answer 1

【答案】（1）2m﹣1；（2）C2：y＝x2﹣4x；（3）0＜a或a≥1或a≤﹣．

【解析】

（1）C1：y＝ax22ax3a＝a（x1）24a，顶点（1，4a）围绕点P（m，0）旋转180°的对称点为（2m1，4a），即可求解；（2）分≤t＜1、1≤t≤、t＞三种情况，分别求解,（3）分a＞0、a＜0两种情况，分别求解．

解：（1）C1：y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，

顶点（1，﹣4a）围绕点P（m，0）旋转180°的对称点为（2m﹣1，4a），

C2：y＝﹣a（x﹣2m+1）2+4a，函数的对称轴为：x＝2m﹣1，

t＝2m﹣1，

故答案为：2m﹣1；

（2）a＝﹣1时，

C1：y＝﹣（x﹣1）2+4，

①当≤t＜1时，

x＝时，有最小值y2＝，

x＝t时，有最大值y1＝﹣（t﹣1）2+4，

则y1﹣y2＝﹣（t﹣1）2+4﹣＝1，无解；

②1≤t≤时，

x＝1时，有最大值y1＝4，

x＝时，有最小值y2＝﹣（t﹣1）2+4，

y1﹣y2＝≠1（舍去）；

③当t＞时，

x＝1时，有最大值y1＝4，

x＝t时，有最小值y2＝﹣（t﹣1）2+4，

y1﹣y2span>＝（t﹣1）2＝1，

解得：t＝0或2（舍去0），

故C2：y＝（x﹣2）2﹣4＝x2﹣4x；

（3）m＝0，

C2：y＝﹣a（x+1）2+4a，

点A、B、D、A′、D′的坐标分别为（1，0）、（﹣3，0）、（0，3a）、（0，1）、（﹣3a，0），

当a＞0时，a越大，则OD越大，则点D′越靠左，

当C2过点A′时，y＝﹣a（0+1）2+4a＝1，解得：a＝，

当C2过点D′时，同理可得：a＝1，

故：0＜a≤或a≥1；

当a＜0时，

当C2过点D′时，﹣3a＝1，解得：a＝﹣，

故：a≤﹣；

综上，故：0＜a≤或a≥1或a≤﹣．