题目内容
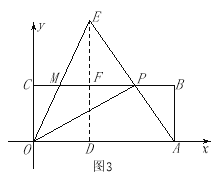
【题目】如图,在直角坐标系![]() 中,矩形
中,矩形![]() 的顶点
的顶点![]() 、
、![]() 分别在
分别在![]() 轴和
轴和![]() 轴正半轴上,点
轴正半轴上,点![]() 的坐标是
的坐标是![]() ,点
,点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 、点
、点![]() 重合),连结
重合),连结![]() 、
、![]() ,过点
,过点![]() 作射线
作射线![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 边于点
边于点![]() ,且
,且![]() ,令
,令![]() ,
,![]() .
.

(1)当![]() 为何值时,
为何值时,![]() ?
?
(2)求![]() 与
与![]() 的函数关系式,并写出
的函数关系式,并写出![]() 的取值范围;
的取值范围;
(3)在点![]() 的运动过程中,是否存在
的运动过程中,是否存在![]() ,使
,使![]() 的面积与
的面积与![]() 的面积之和等于
的面积之和等于![]() 的面积.若存在,请求
的面积.若存在,请求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)当![]() 时,
时,![]() ;(2)
;(2)![]() (
(![]() );(3)存在,
);(3)存在,![]() .
.
【解析】
试题分析:(1)由题意可知,当OP⊥AP时,![]() ∽
∽![]() ,∴
,∴![]() ,即
,即![]() ,于是解得x值;(2)根据已知条件利用两角对应相等两个三角形相似,证明三角形OCM和三角形PCO相似,得出对应边成比例即可得出结论;(3)假设存在x符合题意. 过
,于是解得x值;(2)根据已知条件利用两角对应相等两个三角形相似,证明三角形OCM和三角形PCO相似,得出对应边成比例即可得出结论;(3)假设存在x符合题意. 过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,由
,由![]() 与
与![]() 面积之和等于
面积之和等于![]() 的面积,∴
的面积,∴![]() .然后求出ED,EF的长,再根据三角形相似:
.然后求出ED,EF的长,再根据三角形相似:![]() ∽
∽![]() ,求出MP的长,进而由上题的关系式
,求出MP的长,进而由上题的关系式![]() 求出符合条件的x.
求出符合条件的x.
试题解析:(1)证明三角形OPC和三角形PAB相似是解决问题的关键,由题意知,![]() ,BC∥OA,∵
,BC∥OA,∵![]() ,∴
,∴![]() .∴
.∴![]() .∴
.∴![]() ∽
∽![]() ,∴
,∴![]() ,即
,即![]() ,解得
,解得![]() (不合题意,舍去). ∴当
(不合题意,舍去). ∴当![]() 时,
时,![]() ;(2)由题意可知,
;(2)由题意可知,![]() ∥
∥![]() ,∴
,∴![]() .∵
.∵![]() (已知),∴
(已知),∴![]() . ∵
. ∵![]() ,∴
,∴![]() ∽
∽![]() ,∴对应边成比例:
,∴对应边成比例:![]() ,即
,即![]() . ∴
. ∴![]() ,因为点
,因为点![]() 是
是![]() 边上一动点(不与点
边上一动点(不与点![]() 、点
、点![]() 重合),且满足
重合),且满足![]() ∽
∽![]() ,所以
,所以![]() 的取值范围是
的取值范围是![]() .(3)假设存在
.(3)假设存在![]() 符合题意. 如图
符合题意. 如图![]() 所示,过
所示,过![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() , 则
, 则![]() .∵
.∵![]() 与
与![]() 面积之和等于
面积之和等于![]() 的面积,∴
的面积,∴![]() . ∴
. ∴![]() . ∵
. ∵![]() ∥
∥![]() ,∴
,∴![]() ∽
∽![]() . ∴
. ∴![]() . 即
. 即![]() ,解得
,解得![]() . 因为由(2)得
. 因为由(2)得![]() ,所以
,所以![]() . 解得
. 解得![]() (不合题意舍去). ∴在点
(不合题意舍去). ∴在点![]() 的运动过程中存在x,,使
的运动过程中存在x,,使![]() 与
与![]() 面积之和等于
面积之和等于![]() 的面积,此时
的面积,此时![]() .
.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目