��Ŀ����
����Ŀ����1����֪����ͼ1��![]() Ϊ�ȱ������Σ���
Ϊ�ȱ������Σ���![]() Ϊ
Ϊ![]() ���ϵ�һ���㣨��
���ϵ�һ���㣨��![]() ����
����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ�����ȱ�
Ϊ�����ȱ�![]() ������
������![]() .��֤����
.��֤����![]() ����
����![]() ��
��
��2����ͼ2����![]() �У�
��![]() ��
��![]() ����
����![]() Ϊ
Ϊ![]() �ϵ�һ���㣨��
�ϵ�һ���㣨��![]() ����
����![]() ��
��![]() �غϣ�����
�غϣ�����![]() Ϊ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����ʱ�뷽�����У�������
����ʱ�뷽�����У�������![]() ������⣨1����������룺��
������⣨1����������룺��![]() �Ķ��������߶�
�Ķ��������߶�![]() ��
��![]() ��
��![]() ֮��Ĺ�ϵ����˵�����ɣ�
֮��Ĺ�ϵ����˵�����ɣ�
��3����ͼ3���ڣ�2���������£���![]() ����
����![]() ���ӳ������˶�����
���ӳ������˶�����![]() Ϊ��������
��������![]() ��
��![]() ������
������![]() ��
��![]() ��
��![]() ����ʱ�뷽�����У�������
����ʱ�뷽�����У�������![]() .
.
�����⣨2���Ľ��ۻ���������ֱ��д����������֤��
������![]() ����
����![]() ��
��![]() ��ֱ��д��
��ֱ��д��![]() �ij�.
�ij�.
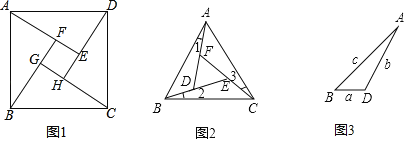
���𰸡���1�������������ڡ�DCE��120������2����DCE��90��, BD2+CD2��DE2��֤������������3������2���еĽ��ۻ���������AE��![]() .
.
��������
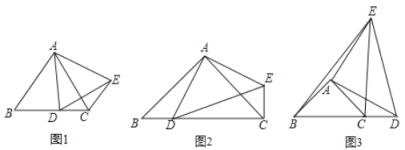
��1���ٸ��ݵȱ������ε����ʾͿ��Եó���BAC=��DAE=60����AB=BC=AC��AD=DE=AE�������Ϳ��Եó���ABD�ա�ACE�����ɵó����ۣ�������ABD�ա�ACE���Լ��ȱ������ε����ʣ��Ϳ��Եó���DCE��120����
��2�����ж���ABD�ա�ACE��SAS�����ó���B=��ACE=45����BD=CE����Rt��DCE�У����ݹ��ɶ����ó�CE2+CD2=DE2�����ɵõ�BD2+CD2=DE2��
��3�������ã�2���еķ����ó�BD2+CD2=DE2���ڸ���Rt��BCE�У�BE=10��BC=6�����![]() �����ó�CD=8-6=2����Rt��DCE�У����
�����ó�CD=8-6=2����Rt��DCE�У����![]() ��������ADE�ǵ���ֱ�������Σ����ɵó�AE�ij���
��������ADE�ǵ���ֱ�������Σ����ɵó�AE�ij���
��1������ͼ1���ߡ�ABC����ADE�ǵȱ������Σ�
��AB��AC��AD��AE���� ACB����B�� 60����
��BAC����DAE��60����
���BAC����DAC����DAE����DAC��
���BAD����EAC��
����ABD����ACE��
 ��
��
���ABD�ա�ACE��SAS����
��BD��CE��
�ڡߡ�ABD�ա�ACE ,
��ACE����B��60��,
���DCE����ACE +��ACB��60��+60����120����
��2����DCE��90��, BD2+CD2��DE2��
֤������ͼ2���ߡ�BAC����DAE��90����
���BAC����DAC����DAE����DAC��
����BAD����CAE��
����ABD����ACE��
 ��
��
���ABD�ա�ACE��SAS����
���B����ACE��45����BD��CE��
���B+��ACB����ACE+��ACB��90����
���BCE��90����
��Rt��DCE��CE2+CD2��DE2��
��BD2+CD2��DE2��
��3���٣�2���еĽ��ۻ�������
���ɣ���ͼ3���ߡ�BAC=��DAE=90����
���BAC+��DAC=��DAE+��DAC��
����BAD=��CAE��
����ABD����ACE��
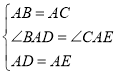
���ABD�ա�ACE��SAS����
���ABC=��ACE=45����BD=CE��
���ABC+��ACB=��ACE+��ACB=90����
���BCE=90��=��ECD��
��Rt��DCE��CE2+CD2=DE2��
��BD2+CD2=DE2
�ڡ�Rt��BCE�У�BE=10��BC=6��
![]()
��BD=CE=8��
��CD=8-6=2��
��Rt��DCE��
![]()
�ߡ�ADE�ǵ���ֱ�������Σ�
![]()

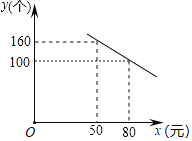
����Ŀ�����ܶ������ϲ����ͷ��Ʒ���ã���Ӱ�����彡���ָ���ͥ���Ӳ���Ҫ�Ŀ�����Ϊ��ij����ѧ��ȤС��Ա���ͬѧһ��������Ʒ����������˵��飬���¿ɷ�Ϊ���֣�A����ˮ��B��ƿװ��Ȫˮ��C��̼�����ϣ�D����̼�����ϣ�����ͳ�ƽ��������������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ�������������
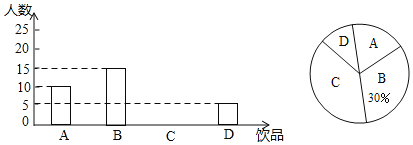
��1������༶�ж�����ͬѧ������ȫ����ͳ��ͼ��
��2�����ð�ͬѧÿ��ÿ��ֻ����һ����Ʒ��ÿ�ֽ���һƿ���۸����±�������ð�ͬѧÿ��������Ʒ���˾������Ƕ���Ԫ��
��Ʒ���� | ��ˮ | ƿװ��Ȫˮ | ̼������ | ��̼������ |
ƽ���۸�Ԫ/ƿ�� | 0 | 2 | 3 | 4 |
��3��Ϊ���������õ�����ϰ�ߣ������ξ��������ð�ˮ��5����ί�ɲ�����������λ���ΪA��B��������λ��ΪC��D��E���������ȡ2����ί�ɲ�������ϰ�ලԱ�������б�������״ͼ�ķ������ǡ�ó鵽2����ĸ��ʣ�