题目内容
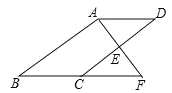
【题目】(2016浙江省温州市第19题)如图,E是ABCD的边CD的中点,延长AE交BC的延长线于点F.
(1)求证:△ADE≌△FCE.
(2)若∠BAF=90°,BC=5,EF=3,求CD的长.
【答案】(1)、证明过程见解析;(2)、8.
【解析】
试题分析:(1)、由平行四边形的性质得出AD∥BC,AB∥CD,证出∠DAE=∠F,∠D=∠ECF,由AAS证明△ADE≌△FCE即可;(2)、由全等三角形的性质得出AE=EF=3,由平行线的性质证出∠AED=∠BAF=90°,由勾股定理求出DE,即可得出CD的长.
试题解析:(1)、∵四边形ABCD是平行四边形, ∴AD∥BC,AB∥CD,
∴∠DAE=∠F,∠D=∠ECF, ∵E是ABCD的边CD的中点, ∴DE=CE,
在△ADE和△FCE中,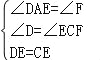 ,∴△ADE≌△FCE(AAS);
,∴△ADE≌△FCE(AAS);
(2)、∵ADE≌△FCE, ∴AE=EF=3, ∵AB∥CD, ∴∠AED=∠BAF=90°,
在ABCD中,AD=BC=5, ∴DE=![]() =
=![]() =4, ∴CD=2DE=8
=4, ∴CD=2DE=8

练习册系列答案
相关题目
【题目】下表记录了甲、乙、丙、丁四名跳远运动员选拔赛成绩的平均数(单位:cm)与方差,要从中选择一名成绩好又发挥稳定的运动员参加决赛,最合适的是( )
甲 | 乙 | 丙 | 丁 | |
平均数 | 610 | 585 | 610 | 585 |
方差 | 12.5 | 13.5 | 2.4 | 5.4 |
A.甲B.乙C.丙D.丁