题目内容
【题目】如图,AB是⊙O的直径,AF是⊙O切线,CD是垂直于AB的弦,垂足为E,过点C作DA的平行线与AF相交于点F,CD=![]() ,BE=2.
,BE=2.

求证:(1)四边形FADC是菱形;
(2)FC是⊙O的切线.
【答案】证明:(1)连接OC,
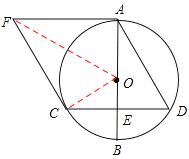
∵AF是⊙O切线,∴AF⊥AB。
∵CD⊥AB,∴AF∥CD。
∵CF∥AD,∴四边形FADC是平行四边形。
∵AB是⊙O的直径,CD⊥AB,
∴![]() 。
。
设OC=x,
∵BE=2,∴OE=x﹣2。
在Rt△OCE中,OC2=OE2+CE2,
∴![]() ,解得:x=4。
,解得:x=4。
∴OA=OC=4,OE=2。∴AE=6。
在Rt△AED中,![]() ,∴AD=CD。
,∴AD=CD。
∴平行四边形FADC是菱形。
(2)连接OF,
∵四边形FADC是菱形,∴FA=FC。
在△AFO和△CFO中,∵ ,∴△AFO≌△CFO(SSS)。
,∴△AFO≌△CFO(SSS)。
∴∠FCO=∠FAO=90°,即OC⊥FC。
∵点C在⊙O上,∴FC是⊙O的切线。
【解析】
试题分析:(1)连接OC,由垂径定理,可求得CE的长,又由勾股定理,可求得半径OC的长,然后由勾股定理求得AD的长,即可得AD=CD,易证得四边形FADC是平行四边形,继而证得四边形FADC是菱形;
(2)连接OF,易证得△AFO≌△CFO,继而可证得FC是⊙O的切线。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
【题目】某摩托车厂本周计划每日生产450辆摩托车,由于工人实行轮休, 每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表: [增加的辆数为正数,减少的辆数为负数]
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | -5 | +7 | -3 | +4 | +10 | -9 | -25 |
(1)本周星期六生产多少辆摩托车?
(2)本周总产量与计划产量相比,是增加了还是减少了?为什么?
(3)产量最多的那天比产量最少的那天多生产多少辆?