题目内容
【题目】△ABC在平面直角坐标系中的位置如图所示.
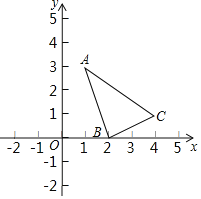
(1)分别写出下列三点坐标:A ,B ,C ;
(2)将△ABC平移至△OB′C′位置,使点A与原点O重合,画出平移后的△OB′C′,写出B′、C′的坐标;
(3)求△OB′C′的面积.
【答案】(1)(1,3)、(2,0)、(4,1);(2)如图所示,△OB′C′即为所求,见解析;B′(1,﹣3)、C′(3,﹣2).(3)△OB′C′的面积为![]() .
.
【解析】
(1)根据点在平面直角坐标系的位置,可分别写出点所对应的坐标即可;
(2)根据平移前后点A与对应点O坐标的位置,可以得出图形△ABC向左平移1个单位、向下平移3个单位,由此可得出平移后点B′、C′的坐标;
(3)利用割补法,把△OB′C′补成一个正方形,减去三个直角三角形的面积计算即可.
(1)由图形知A(1,3),B(2,0),C(4,1);
故答案为:(1,3)、(2,0)、(4,1);
(2)由A(1,3)及其对应点O(0,0)知,需将△ABC向左平移1个单位、向下平移3个单位,
如图所示,△OB′C′即为所求,其中B′(1,﹣3)、C′(3,﹣2),
故答案为:B′(1,﹣3)、C′(3,﹣2);

(3)△OB′C′的面积为3×3﹣![]() ×1×3﹣
×1×3﹣![]() ×3×2﹣
×3×2﹣![]() ×1×2=
×1×2=![]() ,
,
故答案为:![]() .
.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目