题目内容
雅美服装厂现有 种布料
种布料 ,
, 种布料
种布料 ,现计划用这两种布料生产
,现计划用这两种布料生产  、
、 两种型号的时装共
两种型号的时装共 套。已知做一套
套。已知做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元;做一套
元;做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元。若设生产
元。若设生产 型号的时装套数为
型号的时装套数为 ,用这批布料生产这两种型号的时装所获得的总利润为
,用这批布料生产这两种型号的时装所获得的总利润为 元。
元。
(1)请帮雅美服装厂设计出生产方案;
(2)求 (元)与
(元)与 (套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
 种布料
种布料 ,
, 种布料
种布料 ,现计划用这两种布料生产
,现计划用这两种布料生产  、
、 两种型号的时装共
两种型号的时装共 套。已知做一套
套。已知做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元;做一套
元;做一套 型号的时装需用
型号的时装需用 种布料
种布料 ,
, 种布料
种布料 ,可获利润
,可获利润 元。若设生产
元。若设生产 型号的时装套数为
型号的时装套数为 ,用这批布料生产这两种型号的时装所获得的总利润为
,用这批布料生产这两种型号的时装所获得的总利润为 元。
元。(1)请帮雅美服装厂设计出生产方案;
(2)求
 (元)与
(元)与 (套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?
(套)的函数关系,利用一次函数性质,选出(1)中哪个方案所获利润最大?最大利润是多少?(1)方案一: 型号40套,
型号40套, 型号40套;
型号40套;
方案二: 型号39套,
型号39套, 型号41套;
型号41套;
方案三: 型号38套,
型号38套, 型号42套;
型号42套;
方案四: 型号37套,
型号37套, 型号43套;
型号43套;
方案五: 型号36套,
型号36套, 型号44套;
型号44套;
(2)
当 时,即选方案五时,
时,即选方案五时, 有最大值,其最大值为3820元
有最大值,其最大值为3820元
 型号40套,
型号40套, 型号40套;
型号40套;方案二:
 型号39套,
型号39套, 型号41套;
型号41套;方案三:
 型号38套,
型号38套, 型号42套;
型号42套;方案四:
 型号37套,
型号37套, 型号43套;
型号43套;方案五:
 型号36套,
型号36套, 型号44套;
型号44套;(2)

当
 时,即选方案五时,
时,即选方案五时, 有最大值,其最大值为3820元
有最大值,其最大值为3820元试题分析:解:①

由(1)得
 由(2)得x≥40
由(2)得x≥40 .
.
 是整数
是整数  取
取 .)
.)方案一:
 型号40套,
型号40套, 型号40套;
型号40套;方案二:
 型号39套,
型号39套, 型号41套;
型号41套;方案三:
 型号38套,
型号38套, 型号42套;
型号42套;方案四:
 型号37套,
型号37套, 型号43套;
型号43套;方案五:
 型号36套,
型号36套, 型号44套;
型号44套;②


 随
随 的增大而增大
的增大而增大 当
当 时,即选方案五时,
时,即选方案五时, 有最大值,其最大值为3820元。
有最大值,其最大值为3820元。点评:本题难度中等,主要考查学生对解决实际问题时运用二次函数计算与分析。需要根据实际问题的数据进行分析,并运用二次函数的性质及图像求最大值,是这类题型的解题关键。

练习册系列答案
相关题目
 关于y轴对称。
关于y轴对称。
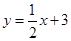 的图象与正比例函数
的图象与正比例函数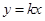 的图象相交于点
的图象相交于点
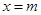 与一次函数的图象交于点B,与正比例函数图象交于点C,若△ABC的面积记为S,求S关于m的函数关系式(写出自变量的取值范围).
与一次函数的图象交于点B,与正比例函数图象交于点C,若△ABC的面积记为S,求S关于m的函数关系式(写出自变量的取值范围). ∠OAB=2。
∠OAB=2。
 与
与 分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样.
分别表示一种白炽灯和一种节能灯的费用y(费用=灯的售价+电费,单位:元)与照明时间x(h)的函数关系图像,假设两种灯的使用寿命都是2000h,照明效果一样. 
 :y=3x+1与直线
:y=3x+1与直线 :y=mx+n相交于点P(1,b).
:y=mx+n相交于点P(1,b).
 ,请你直接写出它的解;
,请你直接写出它的解; :y=nx+m是否也经过点P?请说明理由.
:y=nx+m是否也经过点P?请说明理由. 的图象向上平移2个单位,所得函数图象的解析式为___________.
的图象向上平移2个单位,所得函数图象的解析式为___________. ,梯形APCD的面积为
,梯形APCD的面积为 .
.