��Ŀ����
����Ŀ����գ��������˵������
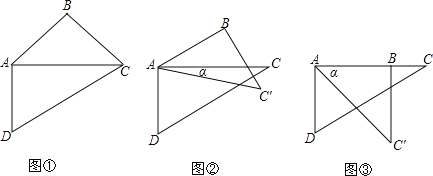
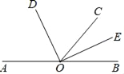
��ͼ����֪��A��O��B��ͬһ��ֱ���ϣ�OEƽ�֡�BOC����DOE��90��
��֤��OD�ǡ�AOC��ƽ���ߣ�
֤������ͼ����ΪOE�ǡ�BOC��ƽ���ߣ�
���ԡ�BOE����COE����������
����DOE��90��
���ԡ�DOC+�ϡ�����90��
�ҡ�DOA+��BOE��180�㩁��DOE�������㣮
���ԡ�DOC+�ϡ�������DOA+��BOE��
���ԡ��������ϡ�����
����OD�ǡ�AOC��ƽ���ߣ�
���𰸡���ƽ���߶��壻COE��90��COE��DOC��DOA��
��������
������֪�����۲�ͼ�Σ����ý�ƽ���ߵ����ʼ���֤��.
֤������ͼ����ΪOE�ǡ�BOC��ƽ���ߣ�
���ԡ�BOE����COE����ƽ���߶��壩
��Ϊ��DOE��90�㣬
���ԡ�DOC����COE��90�㣬
�ҡ�DOA����BOE��180�㩁��DOE��90�㣮
���ԡ�DOC����COE����DOA����BOE��
���ԡ�DOC����DOA��
����OD�ǡ�AOC��ƽ���ߣ�
�ʴ�Ϊ����ƽ���߶��壻COE��90��COE��DOC��DOA��

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ