题目内容
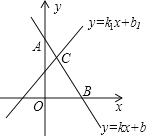
【题目】如图，在平面直角坐标系中，直线
分别与x轴和y轴交于点A和点B.P是线段AB上一动点(不与A、B重合)，过点P分别作PC⊥y轴于点C，PD⊥x轴于点D.设点P的横坐标为m.
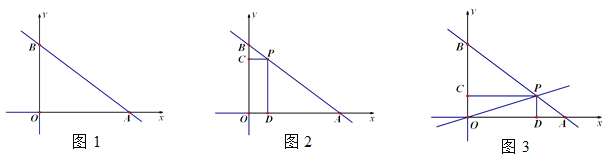
(1)如图1，求线段AB的长度；
(2)如图2，当
时，求点P的坐标；
(3)如图3，作直线OP，若直线OP的解析式为
，求四边形OCPD的周长.
【答案】（1）5；（2）P（1，
）（3）
【解析】
（1）根据解析式求出A,B的坐标即可求出AB的长度；
（2）先求出CP的长为1，故P点横坐标为1，代入解析式求出P点坐标；
（3）联立两函数求出P的坐标，即可求出四边形OCPD的周长.
（1）令x=0，得y=3,∴B（0,3）
令y=0.解得x=4，∴A(4,0)
∴AB=
(2) 
=1,
把x=1代入
得y=
∴P（1，）
（3）联立两函数，即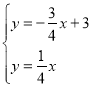
解得
∴P（3，
）
∴四边形OCPD的周长为
练习册系列答案
相关题目
