Question

【题目】已知双曲线：与抛物线：y=ax2+bx+c交于A（2，3）、B（m，2）、C（﹣3，n）三点．

（1）求双曲线与抛物线的解析式；

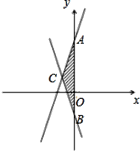
（2）在平面直角坐标系中描出点A、点B、点C，并求出△ABC的面积．

Answer 1

【答案】（1）y=，y=﹣x2+x+3；（2）5.

【解析】分析：（1）函数图象过某一点时，这点就满足关系式，利用待定系数法分别求出反比例函数与二次函数解析式即可；

（2）根据A，B，C三点的坐标可以得出△ADB，△BCE和梯形ADEC的面积，用梯形面积减去两三角形面积即可得到△ABC的面积．

详解：（1）把点A（2，3）代入得：k=6，

∴y=，

把B（m，2）、C（﹣3，n）分别代入y=得，

m=3，n=﹣2，

把A（2，3）、B（3，2）、C（﹣3，﹣2）分别代入y=ax2+bx+c得：

，

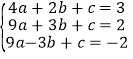解得：，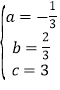

∴抛物线的解析式为：y=﹣x2+x+3；

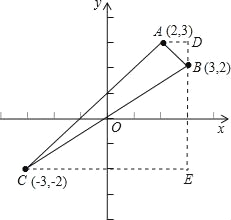
（2）描点画图得：

S△ABC=S梯形ADEC﹣S△ADB﹣S△BCE，

=（1+6）×5﹣×1×1﹣×6×4，

=﹣﹣12，

=5．