题目内容
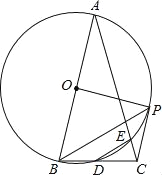
【题目】如图,AB为⊙O的直径,CD切⊙O于点C,与BA的延长线交于点D,OE⊥AB交⊙O于点E,连接CA、CE、CB,CE交AB于点G,过点A作AF⊥CE于点F,延长AF交BC于点P.
(Ⅰ)求∠CPA的度数;
(Ⅱ)连接OF,若AC=![]() ,∠D=30°,求线段OF的长.
,∠D=30°,求线段OF的长.
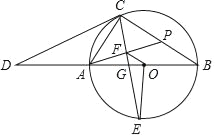
【答案】(Ⅰ)45°;(Ⅱ)![]()
【解析】
(Ⅰ)连接AE,由OA=OB且OE⊥AB知∠OEG+∠AEC=45°,再证∠OEG=∠BAP、∠AEC=∠ABP,在△ABP中利用三角形外角性质可得答案;
(Ⅱ)由切线性质及∠D=30°可得∠AOC=∠OAC=60°,在Rt△ABC中求得BC=3,由∠APC=45°、∠ACP=90°得CP=AC=![]() ,可知BP=3﹣
,可知BP=3﹣![]() ,证OF为△ABP中位线可得答案.
,证OF为△ABP中位线可得答案.
解:(Ⅰ)如图,连接AE,
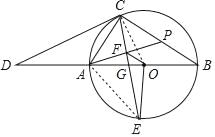
∵OE⊥AB,OA=OE,
∴∠AOE=90°,∠AEO=45°,
∴∠OEG+∠OGE=90°,
∵AF⊥CE,
∴∠AFG=90°,
∴∠FAG+∠AGF=90°,
∵∠AGF=∠OGE,
∴∠OEG=∠BAP,
∵∠AEC=∠ABC,
∴∠APC=∠ABC+∠BAP=∠AEC+∠OEG=∠AEO=45°;
(Ⅱ)连接OC,
∵CD是⊙O的切线,
∴∠DCO=90°,
∵∠D=30°,
∴∠AOC=60°,
∵OA=OC,
∴∠BAC=60°,
在Rt△ABC中,AC=![]() ,
,
∴BC=ACtan∠BAC=![]() ×
×![]() =3,
=3,
由(1)知,AC=CP=![]() ,
,
∴BP=BC﹣CP=3﹣![]() ,
,
∵AF⊥CE,
∴AF=PF,
∵OA=OB,
∴OF=![]() BP=
BP=![]() .
.

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目