题目内容
【题目】如图,抛物线与x轴交于A,B两点,与y轴交于C点,点A的坐标为(2,0),点C的坐标为(0,3),它的对称轴是直线x=-![]() .
.
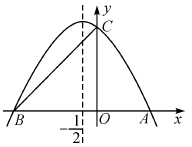
(1)求抛物线的解析式;
(2)M是线段AB上的任意一点,当△MBC为等腰三角形时,求M点的坐标.
【答案】(1)、y=![]() ;(2)、(0,0)或(3
;(2)、(0,0)或(3![]() -3,0)
-3,0)
【解析】
试题分析:(1)、首先将抛物线的解析式设成顶点式,然后将A、C两点坐标代入进行计算;(2)、首先求出点B的坐标,然后分三种情况进行计算.
试题解析:(1)依题意,设抛物线的解析式为y=a![]() +k.由A(2,0),C(0,3)得
+k.由A(2,0),C(0,3)得
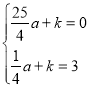 解得
解得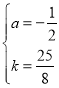 ∴抛物线的解析式为y=
∴抛物线的解析式为y=![]() .
.
(2)当y=0时,有![]() =0. 解得x1=2,x2=-3.∴B(-3,0).
=0. 解得x1=2,x2=-3.∴B(-3,0).
∵△MBC为等腰三角形,则
①当BC=CM时,M在线段BA的延长线上,不符合题意.即此时点M不存在;
②当CM=BM时,∵M在线段AB上,∴M点在原点O上.即M点坐标为(0,0);
③当BC=BM时,在Rt△BOC中,BO=CO=3,由勾股定理得BC=![]() =3
=3![]() ,∴BM=3
,∴BM=3![]() .
.
∴M点坐标为(3![]() -3,0).
-3,0).
综上所述,M点的坐标为(0,0)或(3![]() -3,0).
-3,0).

练习册系列答案
相关题目