题目内容
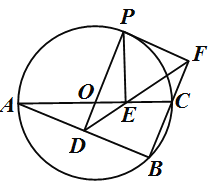
【题目】如图,⊙![]() 是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙
是△ABC的外接圆,AC是直径,过点O作OD⊥AB于点D,延长DO交⊙![]() 于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
于点P,过点P作PE⊥AC于点E,作射线DE交BC的延长线于F点,连接PF。
(1)、若∠POC=60°,AC=12,求劣弧PC的长;(结果保留π)
(2)、求证:OD=OE;
(3)、求证:PF是⊙![]() 的切线。
的切线。
【答案】(1)、2π;(2)、证明过程见解析;(3)、证明过程见解析.
【解析】试题分析:(1)、根据直径得出半径的长度,然后根据弧长的计算公式进行求解;(2)、根据垂直得出∠ADO=∠PEO,对顶角相等,半径相等得出△ADO和△PEO全等,从而得出OD=OE;(3)、连接PC,根据直径得出∠ABC=90°,从而说明PD∥BC,根据已知条件结合(2)得出△PCE和△PFC全等,从而说明∠OPF=90°,得出切线.
试题解析:(1)、由直径AC=12得半径OC=6 劣弧PC的长为![]()
(2)、∵ OD⊥AB,PE⊥AC ∴ ∠ADO=∠PEO=90°
在△ADO和△PEO中,∠ADO=∠PEO,∠AOD=∠POE,OA=OP ∴ △ADO≌△PEO ∴ OD=OE
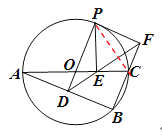
(3)、连接PC,由AC是直径知BC⊥AB,又OD⊥AB, ∴ PD∥BF
∴ ∠OPC=∠PCF,∠ODE=∠CFE 由(2)知OD=OE,则∠ODE=∠OED,又∠OED=∠FEC
∴ ∠FEC=∠CFE ∴ EC=FC 由OP=OC知∠OPC=∠OCE
∴ ∠PCE =∠PCF 在△PCE和△PFC中, EC=FC ∠PCE=∠PCF PC=PC
∴ △PCE≌△PFC ∴ ∠PFC =∠PEC=90° 由∠PDB=∠B=90°可知∠OPF=90°即OP⊥PF
∴ PF是⊙![]() 的切线
的切线

练习册系列答案
相关题目