题目内容
已知二次函数图象的顶点在原点O,对称轴为y轴.一次函数y=kx+1的图象与二次函数的图象交于A,B两点(A在B的左侧) ,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
(1)求一次函数与二次函数的解析式;
(2)判断以线段AB为直径的圆与直线l的位置关系,并给出证明;
(3)把二次函数的图象向右平移2个单位,再向下平移t个单位(t>0),二次函数的图象与x轴交于M,N两点,一次函数图象交y轴于F点.当t为何值时,过F,M,N三点的圆的面积最小,最小面积是多少?
 ,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.(1)求一次函数与二次函数的解析式;
(2)判断以线段AB为直径的圆与直线l的位置关系,并给出证明;
(3)把二次函数的图象向右平移2个单位,再向下平移t个单位(t>0),二次函数的图象与x轴交于M,N两点,一次函数图象交y轴于F点.当t为何值时,过F,M,N三点的圆的面积最小,最小面积是多少?
(1)把A(-4,4)代入y=kx+1
得k=-
,
∴一次函数的解析式为y=-
x+1;
∵二次函数图象的顶点在原点,对称轴为y轴,
∴设二次函数解析式为y=ax2,
把A(-4,4)代入y=ax2
得a=
,
∴二次函数解析式为y=
x2.
(2)由
解得
或
,
∴B(1,
),
过A,B点分别作直线l的垂线,垂足为A',B',
则AA′=4+1=5,BB′=
+1=
.
∴直角梯形AA'B'B的中位线长为
=
,
过B作BH垂直于直线AA'于点H,
则BH=A'B'=5,AH=4-
=
,
∴AB=
=
,
∴AB的长等于AB中点到直线l的距离的2倍,
∴以AB为直径的圆与直线l相切.
(3)平移后二次函数解析式为y=
(x-2)2-t,
令y=0,得
(x-2)2-t=0,x1=2-2
,x2=2+2
,
∵过F,M,N三点的圆的圆心一定在平移后抛物线的对称轴上,点C为定点,B要使圆面积最小,圆半径应等于点F到直线x=2的距离,
此时,半径为2,面积为4π,
设圆心为C,MN中点为E,连CE,CM,则CE=1,
在△CEM中,ME=
=
,
∴MN=2
,而MN=|x2-x1|=4
,
∴t=
,
∴当t=
时,过F,M,N三点的圆面积最小,最小面积为4π.
得k=-
| 3 |
| 4 |
∴一次函数的解析式为y=-
| 3 |
| 4 |
∵二次函数图象的顶点在原点,对称轴为y轴,
∴设二次函数解析式为y=ax2,
把A(-4,4)代入y=ax2

得a=
| 1 |
| 4 |
∴二次函数解析式为y=
| 1 |
| 4 |
(2)由
|
解得
|
|
∴B(1,
| 1 |
| 4 |
过A,B点分别作直线l的垂线,垂足为A',B',
则AA′=4+1=5,BB′=
| 1 |
| 4 |
| 5 |
| 4 |
∴直角梯形AA'B'B的中位线长为
5+
| ||
| 2 |
| 25 |
| 8 |
过B作BH垂直于直线AA'于点H,
则BH=A'B'=5,AH=4-
| 1 |
| 4 |
| 15 |
| 4 |
∴AB=
52+(
|
| 25 |
| 4 |
∴AB的长等于AB中点到直线l的距离的2倍,
∴以AB为直径的圆与直线l相切.
(3)平移后二次函数解析式为y=
| 1 |
| 4 |
令y=0,得
| 1 |
| 4 |
| t |
| t |
∵过F,M,N三点的圆的圆心一定在平移后抛物线的对称轴上,点C为定点,B要使圆面积最小,圆半径应等于点F到直线x=2的距离,
此时,半径为2,面积为4π,
设圆心为C,MN中点为E,连CE,CM,则CE=1,
在△CEM中,ME=
| 22-1 |
| 3 |
∴MN=2
| 3 |
| t |
∴t=
| 3 |
| 4 |
∴当t=
| 3 |
| 4 |

练习册系列答案
相关题目
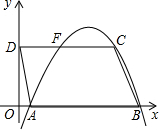 于F,线段AD所在直线的函数解析式为y=-3x+3.
于F,线段AD所在直线的函数解析式为y=-3x+3.
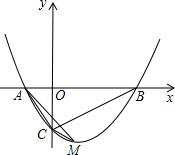 交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求此抛物线的解析式.
交l于点P,M为此抛物线的顶点.若四边形PEMF是有一个内角为60°的菱形,求此抛物线的解析式.
 份x(月)满足的函数关系如图所示.
份x(月)满足的函数关系如图所示.