题目内容
已知抛物线y=ax2-2x+c与它的对称轴相交于点A(1,-4),与y轴交于C,与x轴正半轴交于B.
(1)求这条抛物线的函数关系式;
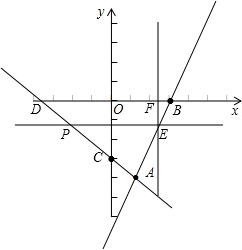
(2)设直线AC交x轴于D,P是线段AD上一动点(P点异于A,D),过P作PE∥x轴交直线AB于E,过E作EF⊥x轴于F,求当四边形OPEF的面积等于
时点P的坐标.
(1)求这条抛物线的函数关系式;
(2)设直线AC交x轴于D,P是线段AD上一动点(P点异于A,D),过P作PE∥x轴交直线AB于E,过E作EF⊥x轴于F,求当四边形OPEF的面积等于
| 7 |
| 2 |
(1)由题意,知点A(1,-4)是抛物线的顶点,
∴
∴a=1,c=-3,
∴抛物线的函数关系式为y=x2-2x-3.
(2)由(1)知,点C的坐标是(0,-3).
设直线AC的函数关系式为y=kx+b,
则
∴b=-3,k=-1,
∴y=-x-3.
由y=x2-2x-3=0,得x1=-1,x2=3,
∴点B的坐标是(3,0).
设直线AB的函数关系式是y=mx+n,
则
解得m=2,n=-6.
∴直线AB的函数关系式是y=2x-6.
设P点坐标为(xP,yP),则yP=-xP-3.
∵PE∥x轴,
∴E点的纵坐标也是-xP-3.
设E点坐标为(xE,yE),
∵点E在直线AB上,
∴-xP-3=2xE-6,
∴xE=
.
∵EF⊥x轴,
∴F点的坐标为(
,0),
∴PE=xE-xP=
,OF=
,EF=-(-xP-3)=xP+3,
∴S四边形OPEF=
(PE+OF)•EF=
(
+
)•(xP+3)=
,
2xP2+3xP-2=0,
∴xP=-2,xP=
,
当y=0时,x=-3,
而-3<-2<1,-3<
<1,
∴P点坐标为(
,-
)和(-2,-1)
∴
|
∴a=1,c=-3,
∴抛物线的函数关系式为y=x2-2x-3.
(2)由(1)知,点C的坐标是(0,-3).
设直线AC的函数关系式为y=kx+b,
则
|
∴b=-3,k=-1,
∴y=-x-3.
由y=x2-2x-3=0,得x1=-1,x2=3,
∴点B的坐标是(3,0).
设直线AB的函数关系式是y=mx+n,
则
|
∴直线AB的函数关系式是y=2x-6.
设P点坐标为(xP,yP),则yP=-xP-3.
∵PE∥x轴,
∴E点的纵坐标也是-xP-3.
设E点坐标为(xE,yE),
∵点E在直线AB上,
∴-xP-3=2xE-6,
∴xE=
| 3-xP |
| 2 |
∵EF⊥x轴,
∴F点的坐标为(
| 3-xP |
| 2 |
∴PE=xE-xP=
| 3-3xP |
| 2 |
| 3-xP |
| 2 |
∴S四边形OPEF=
| 1 |
| 2 |
| 1 |
| 2 |
| 3-3xP |
| 2 |
| 3-xP |
| 2 |
| 7 |
| 2 |
2xP2+3xP-2=0,
∴xP=-2,xP=
| 1 |
| 2 |
当y=0时,x=-3,
而-3<-2<1,-3<
| 1 |
| 2 |
∴P点坐标为(
| 1 |
| 2 |
| 7 |
| 2 |


练习册系列答案
相关题目
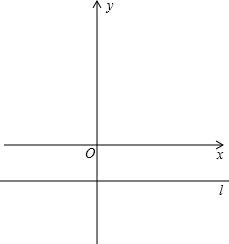 ,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.
,且A点坐标为(-4,4).平行于x轴的直线l过(0,-1)点.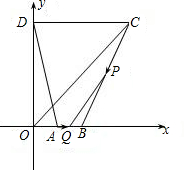 ,若tan∠DAO=2,AB:AO=1:1.
,若tan∠DAO=2,AB:AO=1:1.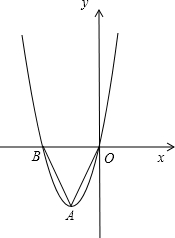

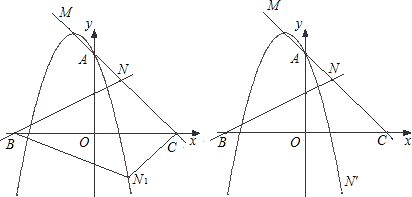
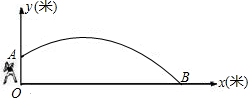 的成绩.(单位:米)
的成绩.(单位:米)