题目内容
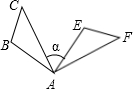
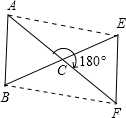
已知:在△ABC中,AB=AC,若将△ABC顺时针旋转180°,得到△FEC.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.
(1)试猜想AE与BF有何关系?说明理由;
(2)若△ABC的面积为3cm2,求四边形ABFE的面积;
(3)当∠ACB为多少度时,四边形ABFE为矩形?说明理由.

(1)∵△FEC是△ABC顺时针旋转180°产生的,
∴ACF、BCE共线且AC=CF,BC=CE(2分),
∴四边形ABFE是平行四边形,
∴AE∥BF且AE=BF.(3分)
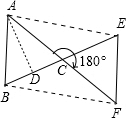 (2)过点A作AD⊥BC于点D,
(2)过点A作AD⊥BC于点D,
则S△ABC=
BC•AD=3cm2.(5分)
又∵平行四边形ABFE中,BC=CE,S△ABC=S△AEC,S△FBC=S△FEC,
又∵AC=CF,
∴S△AEC=S△FBC,
∴四个三角形面积相等,
∴S四边形ABFE=4×S△ABC=12cm2.(6分)
(3)∠ACB=60°时,四边形ABEF是矩形,(7分)
理由:∵当∠ACB=60°时,AB=AC=BC,
∴AF=BE,(8分)
∴四边形ABEF是矩形.(9分)
∴ACF、BCE共线且AC=CF,BC=CE(2分),
∴四边形ABFE是平行四边形,
∴AE∥BF且AE=BF.(3分)
 (2)过点A作AD⊥BC于点D,
(2)过点A作AD⊥BC于点D,则S△ABC=
| 1 |
| 2 |
又∵平行四边形ABFE中,BC=CE,S△ABC=S△AEC,S△FBC=S△FEC,
又∵AC=CF,
∴S△AEC=S△FBC,
∴四个三角形面积相等,
∴S四边形ABFE=4×S△ABC=12cm2.(6分)
(3)∠ACB=60°时,四边形ABEF是矩形,(7分)
理由:∵当∠ACB=60°时,AB=AC=BC,
∴AF=BE,(8分)
∴四边形ABEF是矩形.(9分)

练习册系列答案
相关题目