题目内容
 如图,点D为△ABC内部一点,点E、F、G分别为线段AB、AC、AD上一点,且EG∥BD,GF∥DC
如图,点D为△ABC内部一点,点E、F、G分别为线段AB、AC、AD上一点,且EG∥BD,GF∥DC(1)求证:EF∥BC;
(2)
| AE |
| BE |
| 2 |
| 3 |
| S△EFG |
| S△BCD |
考点:相似三角形的判定与性质,平行线分线段成比例
专题:
分析:(1)先根据相似比的性质得出
=
,
=
,故可得出
=
,由此即可得出结论;
(2)先根据EF∥BC得出∠AEF=∠ABC,再由DG∥BD得出∠AEG=∠ABD,故可得出∠GEF=∠DBC,同理可得,∠GEF=∠DBC,故可得出△EGF∽△BDC根据相似三角形面积的比等于相似比的平方即可得出结论.
| AE |
| EB |
| AG |
| GD |
| AG |
| GD |
| AF |
| FC |
| AE |
| EB |
| AF |
| FC |
(2)先根据EF∥BC得出∠AEF=∠ABC,再由DG∥BD得出∠AEG=∠ABD,故可得出∠GEF=∠DBC,同理可得,∠GEF=∠DBC,故可得出△EGF∽△BDC根据相似三角形面积的比等于相似比的平方即可得出结论.
解答:解:(1)∵EG∥BD,
∴
=
,
∵GF∥DC,
∴
=
,
∴
=
,
∴EF∥BC;

(2)∵EF∥BC,
∴∠AEF=∠ABC,
∵EG∥BD,
∴∠AEG=∠ABD,
∴∠AEF-∠AEG=∠ABC-∠AED,即∠GEF=∠DBC,
同理可得,∠GEF=∠DBC,
∴△EGF∽△BDC,
∵
=
,
∴
=
,
∴
=(
)2=
.
∴
| AE |
| EB |
| AG |
| GD |
∵GF∥DC,
∴
| AG |
| GD |
| AF |
| FC |
∴
| AE |
| EB |
| AF |
| FC |
∴EF∥BC;

(2)∵EF∥BC,
∴∠AEF=∠ABC,
∵EG∥BD,
∴∠AEG=∠ABD,
∴∠AEF-∠AEG=∠ABC-∠AED,即∠GEF=∠DBC,
同理可得,∠GEF=∠DBC,
∴△EGF∽△BDC,
∵
| AE |
| BE |
| 2 |
| 3 |
∴
| EF |
| BC |
| 2 |
| 5 |
∴
| S△EFG |
| S△BCD |
| EF |
| BC |
| 4 |
| 25 |
点评:本题考查的是相似三角形的判定与性质,熟知相似三角形对应边的比等于相似比,面积的比等于相似比的平方是解答此题的关键.

练习册系列答案
相关题目
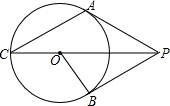 如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为( )
如图,PA、PB是⊙O的切线,A、B分别为切点,PO交圆于点C,若∠APB=60°,PC=6,则AC的长为( )| A、4 | ||
B、2
| ||
C、2
| ||
D、3
|
如果关于x的方程-2x+a=1与
=x+4的解是x=-3,那么字母a的值是( )
| 3x+4 |
| a |
| A、-5 | B、5 | C、0 | D、-5或1 |
 已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).
已知二次函数y=x2+bx+c的图象经过点(4,3),(3,0).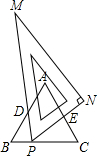 如图,在等边△ABC中,AB=4,当直角三角板MPN的60°角的顶点P在BC上移动时,斜边MP始终经过AB边的中点D,设直角三角板的另一直角边PN与AC相交于点E.设BP=x,CE=y,那么y与x之间的函数图象大致是( )
如图,在等边△ABC中,AB=4,当直角三角板MPN的60°角的顶点P在BC上移动时,斜边MP始终经过AB边的中点D,设直角三角板的另一直角边PN与AC相交于点E.设BP=x,CE=y,那么y与x之间的函数图象大致是( )

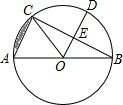 如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6