Question

【题目】填写推理理由，将过程补充完整：

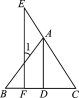
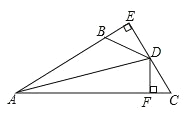
如图，已知AD⊥BC于点D，EF⊥BC于点F，AD平分∠BAC.求证：∠E＝∠1.

证明：∵AD⊥BC，EF⊥BC(已知)，

∴∠ADC＝∠EFC＝90°(垂直的定义)．

∴____________(_____________)．

∴∠1＝_____(_____________)，

∠E＝_____(_______________)．

又∵AD平分∠BAC(已知)，

∴_____＝________．

∴∠1＝∠E(等量代换)．

Answer 1

【答案】见解析

【解析】

由AD垂直于BC，EF垂直于BC，得到一对同位角相等，利用同位角相等两直线平行得到AD与EF平行，利用两直线平行内错角相等得到一对角相等，再由AD为角平分线得到一对角相等，等量代换即可得证．

证明：∵AD⊥BC，EF⊥BC(已知)，

∴∠ADC＝∠EFC＝90°(垂直的定义)．

∴AD∥EF(同位角相等，两直线平行)．

∴∠1＝∠BAD(两直线平行，内错角相等)，

∠E＝∠CAD(两直线平行，同位角相等)．

又∵AD平分∠BAC(已知)，

∴∠BAD＝∠CAD．

∴∠1＝∠E(等量代换)．