题目内容
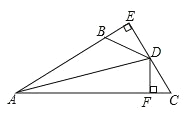
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
【答案】(1)详见解析;(2)12
【解析】
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD、BE=CF,
(1)求证:AD平分∠BAC;(2)已知AC=20, BE=4,求AB的长.
(1)证明:∵DE⊥AB,DF⊥AC,
∴∠E=∠DFC=90°,
∴在Rt△BED和Rt△CFD中
![]()
∴Rt△BED≌Rt△CFD(HL),
∴DE=DF,
∵DE⊥AB,DF⊥AC,
∴AD平分∠BAC;
(2)解:∵Rt△BED≌Rt△CFD,
∴AE=AF,CF=BE=4,
∵AC=20,
∴AE=AF=20﹣4=16,
∴AB=AE﹣BE=16﹣4=12.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
【题目】为了帮助市内一名患“白血病”的中学生,东营市某学校数学社团15名同学积极捐款,捐款情况如下表所示,下列说法正确的是( )
捐款数额 | 10 | 20 | 30 | 50 | 100 |
人数 | 2 | 4 | 5 | 3 | 1 |
A. 众数是100 B. 中位数是30 C. 极差是20 D. 平均数是30