Question

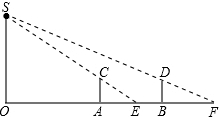
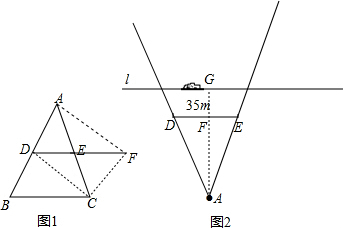
（1）如图1，若D、E分别是△ABC的边AB、AC上的中点，我们把这样的线段DE称为是三角形的中位线．你知道中位线DE与BC之间有什么关系吗？请同学们大胆地猜想一下，并证明你的结论．
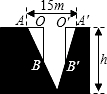
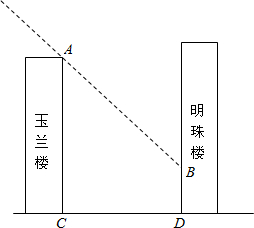
（2）如示意图2，小华家（点A处）和公路（l）之间竖立着一块35m长且平行于公路的巨型广告牌（DE）．广告牌挡住了小华的视线，请在图中画出视点A的盲区，并将盲区内的那段公路计为BC．一辆以60km/h匀速行驶的汽车经过公路段的时间是3s，已知广告牌和公路的距离是40m，求小华家到公路的距离（精确到1m）．

Answer 1

（1）DE∥BC，DE=

1

2

BC
证明：延长DE到F，使EF=DE，连接CF．
∵AE=CE，∠AED=∠CEF，
∴△ADE≌△CEF．
∴AD=CF，∠ADE=∠CFE．
∴AD∥CF．
∵AD=BD，
∴BD=CF．
∴四边形BCFD是平行四边形．
∴DE∥BC，DE=BC．
故答案为三角形的中位线平行于第三边且等于第三边的一半

（2）过A作AE⊥BC于E，交DE于F
∵DE∥BC则△ADE∽△ABC，
设AE=x则

x-40

x

=

35

60000 3600 ×40

，
∴x=

400

3

（7分）
答：小华家到公路的距离是133米；