题目内容
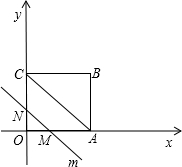
如图,在平面直角坐标系中,四边形OABC是矩形,点B的坐标为(4,3).
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若MN=
AC,求t的值;
②设△OMN的面积为S,当t为何值时,S=
.
(1)直接写出A、C两点的坐标;
(2)平行于对角线AC的直线m从原点O出发,沿x轴正方向以每秒1个单位长度的速度运动,设直线m与矩形OABC的两边分别交于点M、N,设直线m运动的时间为t(秒).
①若MN=
| 1 |
| 2 |
②设△OMN的面积为S,当t为何值时,S=
| 3 |
| 2 |

(1)A(4,0),C(0,3);
(2)①x轴正方向以每秒1个单位长度的速度运动,直线m运动的时间为t时,
可以分为两种情况:
当M、N分别在OA、OC上时,如下图所示:

∵直线m平行于对角线AC
∴△OMN∽△OAC
∴
=
=
=
∴t=2s;
当M、N分别在AB、BC上时,如下图所示:
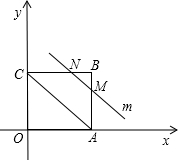
∵直线m平行于对角线AC
∴△BMN∽△BAC
∴
=
=
=
∴t=6
综上所述,当t=2或6时,MN=
AC
②当0<t≤4时,OM=t,
由△OMN∽△OAC,
得
=
,
∴ON=
t,S=
t2=
∴t=2;
当4<t<8时,
如图,∵OD=t,∴AD=t-4.
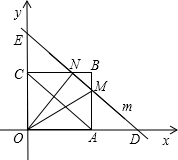
由△DAM∽△AOC,可得AM=
(t-4)
∴BM=6-
t.
由△BMN∽△BAC,可得BN=
BM=8-t
∴CN=t-4
S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积
=12-
(t-4)-
(8-t)(6-
t)-
(t-4)
=-
t2+3t,
∴-
t2+3t=
解得t=4±2
取t=4+2
故当t=2或4+2
时,△OMN的面积S=
.
(2)①x轴正方向以每秒1个单位长度的速度运动,直线m运动的时间为t时,
可以分为两种情况:
当M、N分别在OA、OC上时,如下图所示:

∵直线m平行于对角线AC
∴△OMN∽△OAC
∴
| MN |
| AC |
| OM |
| OA |
| t |
| 4 |
| 1 |
| 2 |
∴t=2s;
当M、N分别在AB、BC上时,如下图所示:

∵直线m平行于对角线AC
∴△BMN∽△BAC
∴
| MN |
| AC |
| BM |
| BA |
| t-4 |
| 4 |
| 1 |
| 2 |
∴t=6
综上所述,当t=2或6时,MN=
| 1 |
| 2 |
②当0<t≤4时,OM=t,
由△OMN∽△OAC,
得
| OM |
| OA |
| ON |
| OC |
∴ON=
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 2 |
∴t=2;
当4<t<8时,
如图,∵OD=t,∴AD=t-4.

由△DAM∽△AOC,可得AM=
| 3 |
| 4 |
∴BM=6-
| 3 |
| 4 |
由△BMN∽△BAC,可得BN=
| 4 |
| 3 |
∴CN=t-4
S=矩形OABC的面积-Rt△OAM的面积-Rt△MBN的面积-Rt△NCO的面积
=12-
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 4 |
| 3 |
| 2 |
=-
| 3 |
| 8 |
∴-
| 3 |
| 8 |
| 3 |
| 2 |
解得t=4±2
| 3 |
取t=4+2
| 3 |
故当t=2或4+2
| 3 |
| 3 |
| 2 |

练习册系列答案
 一线名师提优试卷系列答案
一线名师提优试卷系列答案
相关题目