��Ŀ����
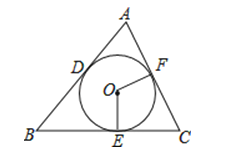
����Ŀ����ͼ��8��8������������ÿ��С�����DZ߳�Ϊ1�������Σ�A��B�Ǹ�㣨�����ߵĽ��㣩��������������ֱ��Ϊ�����ᣬ�������н���ƽ��ֱ������ϵxOy��ʹ��A����Ϊ����2��4����
(1)�������У��������ƽ��ֱ������ϵ��
(2)�ڵڶ������ڵĸ�����ҵ�һ��C��ʹA��B��C���������ABΪ�ױߵĵ��������Σ��������������������C���������� ������������ABC����y��ԳƵġ�A��B��C�䣮

���𰸡�(1)��������(2)����1��1������ͼ������.
��������
��1���ɵ�A����2��4���ɽ���ƽ��ֱ������ϵ��
��2�����ݵ��������εĶ�����ͼ�ɵã��ٷֱ�������A��B��C����y��ĶԳƵ㣬˳�����Ӽ��ɵã�
(1)��ͼ��ʾ������ƽ��ֱ������ϵ��
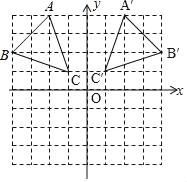
(2)��ͼ��ʾ����ABC��Ϊ�������е�C������Ϊ����1��1������ABC����y��ԳƵġ�A��B��C����ͼ��ʾ��
�ʴ�Ϊ������1��1����

����Ŀ��Ϊ�˽�ѧ����ȫ֪ʶ�����������ѧУ�����ȡ��20��ѧ�����а�ȫ֪ʶ���ԣ����Գɼ�(�ٷ���)���£�
78��86��93��81��97��88��79��93��87��90��93��98��88��81��94��95��81��98��99��94
(1)�����������ݣ������б���������ÿ�麬��Сֵ����
�ɼ�/�� | 70~80 | 80~90 | 90~100 |
���� | 7 |
(2)����(1)��������������ͳ��ͼ�������ʾ��70~80�����ε�Բ�ĽǶ�����
(3)��֪��У����2000��ѧ�������涨�ɼ�90�ּ�����Ϊ���㣬���Ƹ�Уѧ����ȫ֪ʶ�������Ϊ������ж����ˣ�