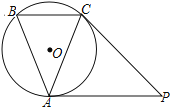
题目内容
【题目】已知:AB=AC,PA=PC,若PA为△ABC的外接圆⊙O的切线
(1) 求证:PC为⊙O的切线;
(2) 连接BP,若sin∠BAC=![]() ,求tan∠BPC的值.
,求tan∠BPC的值.
【答案】(1)见解析;(2)![]()
【解析】分析:(1) 连接OA、OC, 证明△OAP≌△OCP,即可求出![]() 即可证明.
即可证明.
![]() 连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=
连接AO,并延长交BC于D,连接OB、OC,得到BC∥PA,根据sin∠BAC=sin∠BOD=![]() ,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=
,设BD=3,OB=5,则OD=4, 根据sin∠APC=sin∠PCE=![]() ,
,
求出PC=15,CE=12, 过点C作CF⊥BP于F ,证明△BCF∽△BPE,求出![]() 的长即可求解.
的长即可求解.
详解:(1) 连接OA、OC,
∵PA为⊙O的切线,
∴∠OCP=90°,
连接OP,
可证:△OAP≌△OCP(SSS),
∴∠OAP=∠OCP=90°,
∴PC为⊙O的切线,
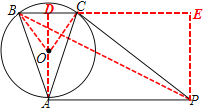
(2) 连接AO,并延长交BC于D,连接OB、OC,
∵AB=AC,OB=OC∴AD为线段BC的垂直平分线,
∴AD⊥BC∵AD⊥AP,
∴BC∥PA,
∵sin∠BAC=sin∠BOD=![]() ∴设BD=3,OB=5,则OD=4,
∴设BD=3,OB=5,则OD=4,
∵∠PAC=∠ACB,且AB=AC,PA=PC,
∴∠BAC=∠APC过点P作PE⊥BC交BC的延长线于E,
∴四边形APED为矩形 ,
∴PE=AD=9 ,
∴sin∠APC=sin∠PCE=![]() ,PC=15,CE=12,
,PC=15,CE=12,
过点C作CF⊥BP于F ,
∵△BCF∽△BPE
∴![]() ,CF=
,CF=![]() ,BF=
,BF=![]() ,PF=
,PF=![]() ∴tan∠BPC=
∴tan∠BPC=![]() .
.

练习册系列答案
相关题目