题目内容
【题目】已知:如图,锐角△ABC的两条高CD、BE相交于点O,且OB=OC
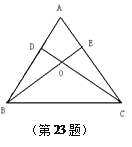
1.求证:△ABC是等腰三角形
2.连结AO,判断AO与BC的位置关系,并说明理由.
【答案】1.见解析;2.AO⊥BC
【解析】
(1)由OB=OC得到∠OBC=∠OCB,在△BCD与△BEC中利用内角和定理以及等量代换即得到∠ABC=∠ACB,故△ABC为等腰三角形
(2)连接AO并延长交BC于F,易证△AOB≌△AOC,得到AF为∠BAC的角平分线,得到OA⊥BC
(1)∵OB=OC,
∴∠OBC=∠OCB,
∵锐角△ABC的两条高BD、CE相交于点O,
∴∠BEC=∠BDC=90°,
∵∠BEC+∠BCE+∠ABC=∠BDC+∠DBC+∠ACB=180°,
∴∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形;
(2)AO⊥BC
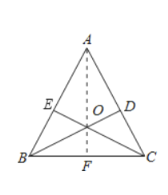
理由:连接AO并延长交BC于F,
∵AB=AC,OB=OC,
又∵OA=OA,
∴△AOB≌△AOC.
∴∠BAF=∠CAF,
∴AF为∠BAC的角平分线
又∵△ABC为等腰三角形
∴OA⊥BC

 出彩同步大试卷系列答案
出彩同步大试卷系列答案【题目】某学校的“图书角”平均每天借出图书 50 册.如果某天借出 51 册,就记作+1;如果某天借出 45 册,就记作-5.上星期该“图书角”借出图书数量记录如下表:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
0 | +10 | +4 | -3 | -6 |
(1)上星期五借出图书多少册?
(2)上星期二比上星期五多借出图书多少册?
(3)上星期平均每天借出图书多少册?
【题目】莒南县欲从某师范院校招聘一名“特岗教师”,对甲、乙、丙、丁四位候选人进行了面试和笔试,他们的成绩如表:
候选人 | 甲 | 乙 | 丙 | 丁 | |
测试成绩 | 面试 | 86 | 91 | 90 | 83 |
笔试 | 90 | 83 | 83 | 92 | |
根据录用程序,作为人民教师面试的成绩应该比笔试的成绩更重要,并分别赋予它们6和4的权.根据四人各自的平均成绩,你认为将录取( )
A.甲B.乙C.丙D.丁