题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE,垂足分别为E、D,AD=2.6cm,DE=1.2cm,求BE的长.

【答案】1.4cm.
【解析】
首先,由题意可知∠BEC=∠CDA=90°,∠BCE和∠ACE、∠ACE和∠DAC互余,从而可得∠BCD=∠DAC;接下来,利用AAS可推得△CEB≌△ADC,故CE=AD,BE=CD,结合CD=CE-DE即可求出BE的长.
∵BE⊥CE,AD⊥CE,
∴∠BEC=∠CDA=90°.
∴∠ACD+∠DAC=90°.∠ACD+∠BCD=90°.
∴∠BCD=∠DAC.
在△CEB 和△ADC中
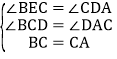
∴△CEB≌△ADC(AAS).
∴CE=AD=2.6cm,
∴BE=CD=CE﹣DE=2.6cm﹣1.2cm=1.4cm.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目







