题目内容
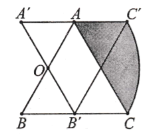
【题目】如图,![]() 是边长为
是边长为![]() 的等边三角形
的等边三角形![]() ,将绕边
,将绕边![]() 的中点
的中点![]() 逆时针旋转
逆时针旋转![]() ,点
,点![]() 的运动路径为
的运动路径为![]() ,则图中阴影部分的面积为__________.
,则图中阴影部分的面积为__________.
【答案】![]()
【解析】
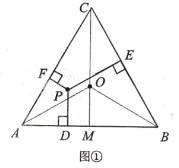
如图,连接OC,OC',设AC于OC'交点为D,由等边三角形的性质和旋转的性质可求OC'=OC=2![]() ,∠COC'=60°,由三角形内角和定理可求∠ADO=90°,由面积的和差关系可求解.
,∠COC'=60°,由三角形内角和定理可求∠ADO=90°,由面积的和差关系可求解.
如图,连接OC,OC',设AC于OC'交点为D,

∵△ABC是边长为4的等边三角形,
∴∠B=∠BAC=60°,AB=BC=4,
∵点O是AB的中点,
∴AO=![]() AB=2,OC⊥AB,
AB=2,OC⊥AB,
∴∠BOC=∠AOC=90°,
∴OC=BCsin60°=2![]() ,
,
∵将△ABC绕边AB的中点O逆时针旋转60°,
∴OC'=OC=2![]() ,∠COC'=60°,
,∠COC'=60°,
∴∠AOC'=∠AOC-∠COC'=30°,
∴∠ADO=180°-∠AOC'-∠BAC=90°,
∴AD=AOsin30°=1,
∴S阴影=S扇形C'OC+S△AOC′-S△AOC
![]()
=![]() ,
,
故答案为:![]() .
.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案【题目】如图,点C是以点O为圆心,AB为直径的半圆上的动点(不与点A,B重合),AB=6cm,过点C作CD⊥AB于点D,E是CD的中点,连接AE并延长交![]() 于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.
于点F,连接FD.小腾根据学习函数的经验,对线段AC,CD,FD的长度之间的关系进行了探究.

下面是小腾的探究过程,请补充完整:
(1)对于点C在![]() 上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
上的不同位置,画图、测量,得到了线段AC,CD,FD的长度的几组值,如表:
位置1 | 位置2 | 位置3 | 位置4 | 位置5 | 位置6 | 位置7 | 位置8 | |
AC/cm | 0.1 | 0.5 | 1.0 | 1.9 | 2.6 | 3.2 | 4.2 | 4.9 |
CD/cm | 0.1 | 0.5 | 1.0 | 1.8 | 2.2 | 2.5 | 2.3 | 1.0 |
FD/cm | 0.2 | 1.0 | 1.8 | 2.8 | 3.0 | 2.7 | 1.8 | 0.5 |
在AC,CD,FD的长度这三个量中,确定 的长度是自变量, 的长度和 的长度都是这个自变量的函数;

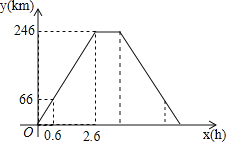
(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;
(3)结合函数图象,解答问题:当CD>DF时,AC的长度的取值范围是 .
【题目】某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 | 人数 | 占女生人数百分比 |
| 4 |
|
|
|
|
| 5 |
|
| 6 |
|
| 2 |
|
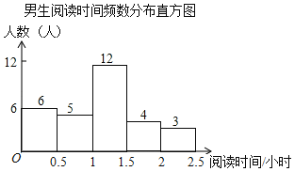
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中,![]() ,
,![]() ;
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在2~2.5小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?