题目内容
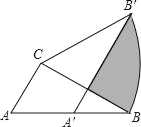
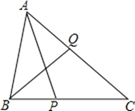
【题目】如图,在△ABC中,![]() ,
,![]() ,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:
,P、Q分别在BC、CA上,并且AP、BQ分别是∠BAC、∠ABC的角平分线.求证:
(1)![]() ;
;
(2)![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)由三角形的内角和就可以得出∠ABC=80°,再由角平分线的性质就可以得出∠QBC=40°,就有∠QBC=∠C而得出结论;
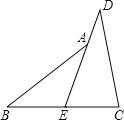
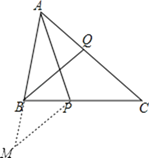
(2)延长AB至M,使得BM=BP,连结MP,根据条件就可以得出∠M=∠C,进而证明△AMP≌△ACP就可以得出结论.
(1)∵BQ是![]() 的角平分线,
的角平分线,
∴![]() .
.
∵![]() ,且
,且![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)延长AB至M,使得![]() ,连结MP.
,连结MP.
∴![]() ,
,
∵△ABC中![]() ,
,![]() ,
,
∴![]() ,
,
∵BQ平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵AP平分![]() ,
,
∴![]() ,
,
在△AMP和△ACP中,
∵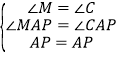 ,
,
∴△AMP≌△ACP,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]()

练习册系列答案
相关题目