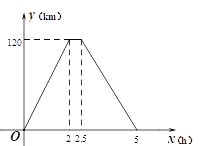
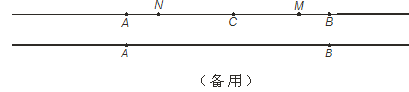
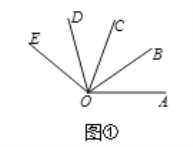
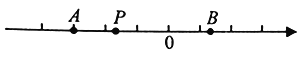题目内容

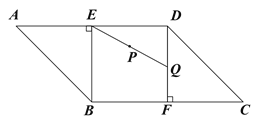
【题目】如图，已知平行四边形ABCD中，AD = 6，AB = ，∠A = 45°．过点B、D分别做BE⊥AD，DF⊥BC，交AD、BC与点E、F．点Q为DF边上一点，∠DEQ = 30°，点P为EQ的中点，过点P作直线分别与AD、BC相交于点M、N．若MN = EQ，则EM的长等于___________．

【答案】1或2

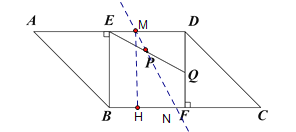
【解析】分析：分两种情况进行讨论：①如图所示： 易得 则 四边形是正方形. 过点作于点易证明≌ 可得 ②如图所示：

参照①可得可得

是等腰三角形，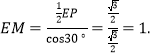

详解：①如图所示： 易得 则 四边形是正方形. 过点作于点易证明≌ 可得

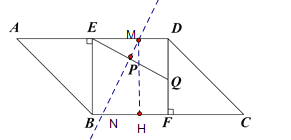
②如图所示：参照①可得可得

是等腰三角形，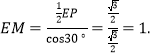

故答案为：1或2.

练习册系列答案
相关题目

【题目】在一次运输任务中，一辆汽车将一批货物从甲地运往乙地，到达乙地卸货后返回甲地.设汽车从甲地出发x（h）时，汽车与甲地的距离为y（km），y与x的关系如图所示.

根据图像回答下列问题:

（1）汽车在乙地卸货停留 （h）；

（2）求汽车返回甲城时y与x的函数解析式，并写出定义域；

（3）求这辆汽车从甲地出发4 h时与甲地的距离.

【题目】已知：，且、、分别是点A. B. C在数轴上对应的数．

（1）写出=___；=___；=___.

（2）若甲、乙、丙三个动点分别从A.B.C三点同时出发沿数轴负方向运动,它们的速度分别是1、2、4,(单位/秒),运行秒后,甲、乙、丙三个动点对应的位置分别为：，，,当时,求式子的值．

（3）若甲、乙、丙三个动点分别从A，B，C三点同时出发沿数轴正方向运动,它们的速度分别是1，2，4（单位/秒），运动多长时间后，乙与甲、丙等距离？

【题目】已知线段AB=m(m为常数)，点C为直线AB上一点（不与点A、B重合），点M、N分别在线段BC、AC上，且满足CN=3AN，CM=3BM.

(1)如图，当点C恰好在线段AB中点，且m=8时，则MN=______；

(2) 若点C在点A左侧，同时点M在线段AB上(不与端点重合)，请判断CN+2AM -2MN的值是否与m有关？并说明理由.

(3) 若点C是直线AB上一点（不与点A、B重合），同时点M在线段AB上(不与端点重合)，求MN长度 (用含m的代数式表示).

【题目】（建立概念）如下图，A、B为数轴上不重合的两定点，点P也在该数轴上，我们比较线段和的长度，将较短线段的长度定义为点P到线段的“靠近距离”.特别地，若线段和的长度相等，则将线段或的长度定义为点P到线段的“靠近距离”.

（概念理解）如下图，数轴的原点为O，点A表示的数为，点B表示的数为4.

（1）点O到线段的“靠近距离”为________；

（2）点P表示的数为m，若点P到线段的“靠近距离”为3，则m的值为_________；

（拓展应用）（3）如下图，在数轴上，点P表示的数为，点A表示的数为，点B表示的数为6. 点P以每秒2个单位长度的速度向正半轴方向移动时，点B同时以每秒1个单位长度的速度向负半轴方向移动.设移动的时间为秒，当点P到线段的“靠近距离”为3时，求t的值.

【题目】某次篮球联赛中，两队的积分如下表所示：

队名

比赛场次

胜场场次

负场场次

积分

前进

14

10

4

24

钢铁

14

0

14

14

请回答下列问题：

（1）负一场_________积分；

（2）求胜一场积多少分？

（3）某队的胜场总积分比负场总积分的3倍多3分，求该队胜了多少场？

【题目】某校组织360名师生外出活动，计划租用甲、乙两种型号的客车；经了解，甲车每辆最多能载40人和16件行李，乙车每辆最多能载30人和20件行李．

（1）已知师生行李打包后共有164件，若租用10辆甲、乙两种型号的客车，请你帮助设计出该校所有可行的租车方案；

（2）若师生行李打包后共有m件，且170 < m ≤ 184，如果所租车辆刚好把所有师生和行李载走（每辆车均以最多承载量载满），求m的值．

【题目】若的度数是的度数的k倍，则规定是的k倍角.

（1）若∠M=21°17'，则∠M的5倍角的度数为 ；

（2）如图1，OB是∠AOC的平分线，OD是∠COE的平分线，若∠AOC=∠COE，请直接写出图中∠AOB的所有3倍角；

（3）如图2，若∠AOC是∠AOB的5倍角，∠COD是∠AOB的3倍角，且∠AOC和∠BOD互为补角，求∠AOD的度数.

【题目】如图，四边形ABCD中，AC，BD相交于点O，O是AC的中点，AD//BC，AC=8,BD=6.

（1）求证：四边形ABCD是平行四边形；

（2）若AC⊥BD，求□ABCD的面积.

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网