题目内容
【题目】如图O是边长为9的等边三角形ABC内的任意一点,且OD∥BC,交AB于点D,OF∥AB,交AC于点F,OE∥AC,交BC于点E,则OD+OE+OF的值为( )
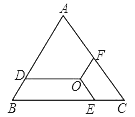
A. 3 B. 6 C. 8 D. 9
【答案】D
【解析】
根据等边三角形,平行线的性质,和平行四边形的判定,并根据等腰梯形性质求解.
延长OD交AC于点G,
∵OE∥CG,OG∥CE,
∴四边形OGCE是平行四边形,有OE=CG,∠OGF=∠C=60°,
∵OF∥AB,
∴∠OFG=∠A=60°,
∴OF=OG,
∴△OGF是等边三角形,
∴OF=FG,
∵OD∥BC,
∴∠ADO=∠B=60°,
∴梯形OFAD是等腰梯形,有OD=AF,即OD+OE+OF=AF+FG+CG=AC=9.
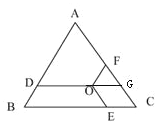
故选:D

练习册系列答案
相关题目