题目内容
如图,已知点 从
从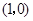 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿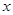 轴向正方向运动,以
轴向正方向运动,以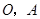 为顶点作菱形
为顶点作菱形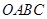 ,使点
,使点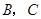 在第一象限内,且
在第一象限内,且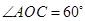 ;以
;以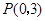 为圆心,
为圆心,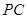 为半径作圆.设点
为半径作圆.设点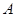 运动了
运动了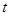 秒,求:
秒,求:
(1)点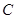 的坐标(用含
的坐标(用含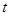 的代数式表示);
的代数式表示);
(2)当点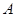 在运动过程中,所有使
在运动过程中,所有使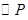 与菱形
与菱形 的边所在直线相切的
的边所在直线相切的 的值.
的值.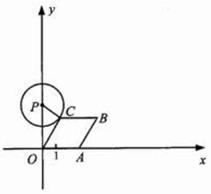
 从
从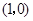 出发,以1个单位长度/秒的速度沿
出发,以1个单位长度/秒的速度沿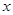 轴向正方向运动,以
轴向正方向运动,以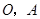 为顶点作菱形
为顶点作菱形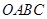 ,使点
,使点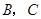 在第一象限内,且
在第一象限内,且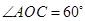 ;以
;以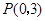 为圆心,
为圆心,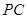 为半径作圆.设点
为半径作圆.设点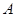 运动了
运动了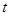 秒,求:
秒,求:(1)点
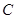 的坐标(用含
的坐标(用含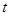 的代数式表示);
的代数式表示);(2)当点
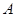 在运动过程中,所有使
在运动过程中,所有使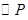 与菱形
与菱形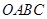 的边所在直线相切的
的边所在直线相切的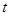 的值.
的值.
解:(1)过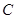 作
作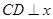 轴于
轴于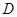 ,
,
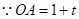 ,
,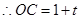 ,
,
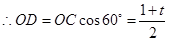 ,
,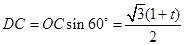 ,
,
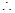 点
点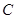 的坐标为
的坐标为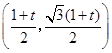 .
.
(2)①当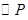 与
与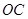 相切时(如图1),切点为
相切时(如图1),切点为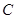 ,此时
,此时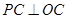 ,
,
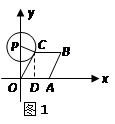
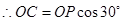 ,
,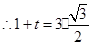 ,
,
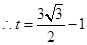 .
.
②当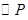 与
与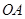 ,即与
,即与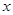 轴相切时(如图2),则切点为
轴相切时(如图2),则切点为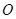 ,
,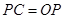 ,
,
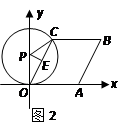
过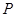 作
作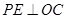 于
于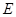 ,则
,则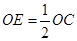 ,
,
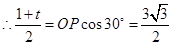 ,
,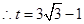 .
.
③当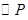 与
与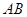 所在直线相切时(如图3),设切点为
所在直线相切时(如图3),设切点为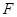 ,
,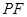 交
交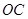 于
于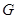 ,
,
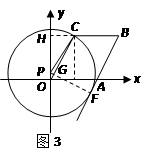
则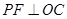 ,
,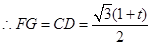 ,
,
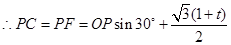 .
.
过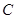 作
作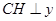 轴于
轴于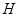 ,则
,则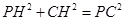 ,
,
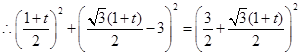 ,
,
化简,得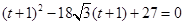 ,
,
解得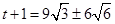 ,
,
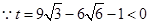 ,
,
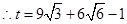 .
.
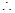 所求
所求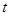 的值是
的值是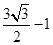 ,
,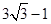 和
和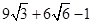 .
.
 作
作 轴于
轴于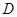 ,
,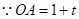 ,
,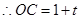 ,
,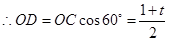 ,
,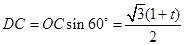 ,
, 点
点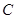 的坐标为
的坐标为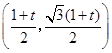 .
.(2)①当
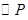 与
与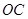 相切时(如图1),切点为
相切时(如图1),切点为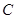 ,此时
,此时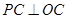 ,
,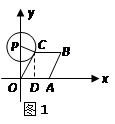
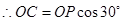 ,
,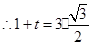 ,
,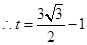 .
.②当
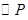 与
与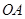 ,即与
,即与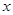 轴相切时(如图2),则切点为
轴相切时(如图2),则切点为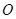 ,
,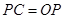 ,
,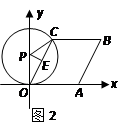
过
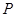 作
作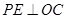 于
于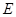 ,则
,则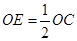 ,
,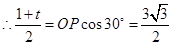 ,
,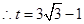 .
.③当
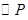 与
与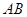 所在直线相切时(如图3),设切点为
所在直线相切时(如图3),设切点为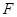 ,
,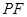 交
交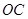 于
于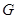 ,
,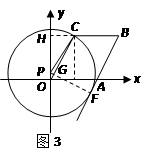
则
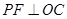 ,
,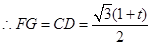 ,
,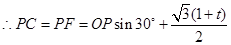 .
.过
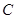 作
作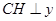 轴于
轴于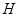 ,则
,则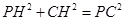 ,
,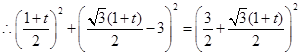 ,
,化简,得
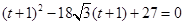 ,
,解得
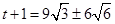 ,
,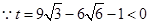 ,
,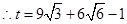 .
.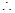 所求
所求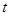 的值是
的值是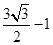 ,
,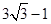 和
和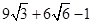 .
.(1)过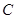 作
作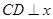 轴于
轴于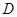 ,利用三角函数求得OD、DC的长,从而求得点
,利用三角函数求得OD、DC的长,从而求得点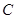 的坐标
的坐标
⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,
等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.
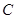 作
作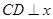 轴于
轴于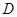 ,利用三角函数求得OD、DC的长,从而求得点
,利用三角函数求得OD、DC的长,从而求得点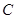 的坐标
的坐标⊙P与菱形OABC的边所在直线相切,则可与OC相切;或与OA相切;或与AB相切,应分三种情况探讨:①当圆P与OC相切时,如图1所示,由切线的性质得到PC垂直于OC,再由OA=+t,根据菱形的边长相等得到OC=1+t,由∠AOC的度数求出∠POC为30°,在直角三角形POC中,利用锐角三角函数定义表示出cos30°=oc/op,表示出OC,
等于1+t列出关于t的方程,求出方程的解即可得到t的值;②当圆P与OA,即与x轴相切时,过P作PE垂直于OC,又PC=PO,利用三线合一得到E为OC的中点,OE为OC的一半,而OE=OPcos30°,列出关于t的方程,求出方程的解即可得到t的值;③当圆P与AB所在的直线相切时,设切点为F,PF与OC交于点G,由切线的性质得到PF垂直于AB,则PF垂直于OC,由CD=FG,在直角三角形OCD中,利用锐角三角函数定义由OC表示出CD,即为FG,在直角三角形OPG中,利用OP表示出PG,用PG+GF表示出PF,根据PF=PC,表示出PC,过C作CH垂直于y轴,在直角三角形PHC中,利用勾股定理列出关于t的方程,求出方程的解即可得到t的值,综上,得到所有满足题意的t的值.

练习册系列答案
相关题目
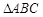 是等边三角形,⊙O过点B,C,且与
是等边三角形,⊙O过点B,C,且与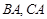 的延长线分别交于点D,E.弦
的延长线分别交于点D,E.弦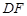 ∥
∥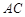 ,
,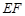 的延长线交
的延长线交 的延长线于点G.
的延长线于点G.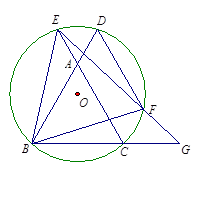
 是等边三角形;
是等边三角形;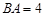 ,
,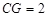 ,求
,求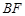 的长.
的长.
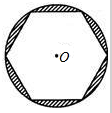
 中,
中,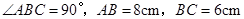 ,分别以
,分别以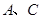 为圆心,以
为圆心,以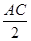 的长为半径作圆,将
的长为半径作圆,将
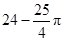
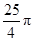
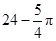
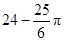
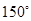 的扇形做成一个圆锥模型的侧面,则此圆锥的高为 cm(结果保留根号).
的扇形做成一个圆锥模型的侧面,则此圆锥的高为 cm(结果保留根号).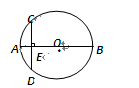
 是
是 的弦,
的弦, 于
于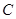 ,若
,若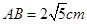 ,
,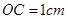 ,则
,则