题目内容
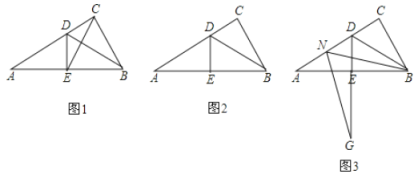
【题目】如图,矩形ABCD中,AD=6,DC=8,矩形EFGH的三个顶点E、G、H分别在矩形ABCD的边ABCD的边AB、CD、DA上,AH=2,连接CF.当△CGF是直角三角形时,线段AE的长为______.

【答案】2或6或![]() 或
或![]()
【解析】
由题意得,分∠FGC和∠FCG和∠GFC为直角讨论,①当∠GFC为90![]() 时,E、F、C三点在同一直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解;
时,E、F、C三点在同一直线上,所以△AEH∽△BCE,根据相似三角形的对应线段成比例可求出解;
②当∠GCF=90![]() ,此时F点正好落在BC上, △AEH≌△CGF, △AEH∽△GDH,可求得AE的值;
,此时F点正好落在BC上, △AEH≌△CGF, △AEH∽△GDH,可求得AE的值;
③当∠CGF=90![]() 时,C,G,H共线,所以不可能.
时,C,G,H共线,所以不可能.
解:①由题意得,∠FGC和∠FCG都不能为直角,当∠GFC为90![]() 时,E、F、C三点在同一直线上,所以△AEH∽△BCE,
时,E、F、C三点在同一直线上,所以△AEH∽△BCE,![]()
![]() ,
,
设AE=x,有![]() ,可得x=2或者x=6,
,可得x=2或者x=6,
②当∠GCF=90![]() ,此时F点正好落在BC上,则△AEH≌△CGF, △AEH∽△GDH,则
,此时F点正好落在BC上,则△AEH≌△CGF, △AEH∽△GDH,则
![]() ,解得x=4+2
,解得x=4+2![]() 或x=4-2
或x=4-2![]() ,
,
③当∠CGF=90![]() 时,C,G,H共线,所以不可能;
时,C,G,H共线,所以不可能;
故答案:2或6或![]() 或
或![]() .
.

练习册系列答案
相关题目
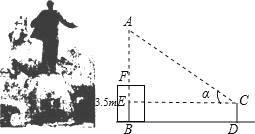
【题目】农八师石河子市某中学初三(1)班的学生,在一次数学活动课中,来到市游憩广场,测量坐落在广场中心的王震将军的铜像高度,已知铜像底座的高为3.5m.某小组的实习报告如下.请你计算出铜像的高(结果精确到0.1m)
实习报告2003年9月25日
题目1 | 测量底部可以到达的铜像高 | |||
| ||||
测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
BD的长 | 12.3m | 11.7m | ||
测倾器CD的高 | 1.32m | 1.28m | ||
倾斜角 | α=30°56' | α=31°4' | ||
计 算 | ||||
结果 | ||||