题目内容
等腰梯形的周长为60,腰长为8,对角线长为24,则连接两腰中点与一底中点的线段组成的三角形的周长为______.
如图,
因为E,F,G分别为AB,BC,CD中点,
所以EF=
AC,FG=
BD,EG=
(AD+BC)
又等腰梯形的周长为60,腰长为8,所以AD+BC=60-8×2=44
AC=BD=24
∴三角形EFG的周长为EF+FG+GE=
AC+
BD+
(AD+BC)=12+12+22=46.
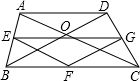
因为E,F,G分别为AB,BC,CD中点,
所以EF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
又等腰梯形的周长为60,腰长为8,所以AD+BC=60-8×2=44
AC=BD=24
∴三角形EFG的周长为EF+FG+GE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


练习册系列答案
 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目





