题目内容
若等腰梯形的两条对角线互相垂直，中位线长为8cm，则该等腰梯形的面积为（ ）cm2．
| A．16 | B．32 | C．64 | D．512 |
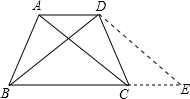
如图，过D点作DE∥AC交BC延长线于E
∵DE∥AC，AD∥BC
∴四边形ACED为平行四边形
∴AD=CE AC=DE
又∵中位线长为8
∴AD+BC=16
∴BE=BC+CE=16
∵AC⊥BD
∴△BDE为等腰直角三角形
∴DE=16×sin45°=8
∴梯形的面积=
×8
×8
=64
故选C．
∵DE∥AC，AD∥BC
∴四边形ACED为平行四边形
∴AD=CE AC=DE
又∵中位线长为8
∴AD+BC=16
∴BE=BC+CE=16
∵AC⊥BD
∴△BDE为等腰直角三角形
∴DE=16×sin45°=8
| 2 |
∴梯形的面积=
| 1 |
| 2 |
| 2 |
| 2 |
故选C．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
端点时，另一点也随之停止运动，设运动的时间为t秒．
