题目内容
【题目】如图1,P(2,2),点A在x轴正半轴上运动,点B在y轴上运动,且PA=PB.
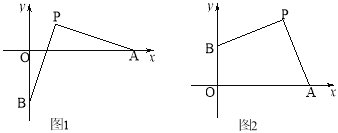
(1)求证:PA⊥PB;
(2)若点A(8,0),求点B的坐标;
(3)求OA – OB的值;
(4)如图2,若点B在y轴正半轴上运动时,直接写出OA+OB的值.
【答案】(1)详见解析;(2)点B的坐标为(0,-4);(3)4;(4)4.
【解析】
试题分析:(1)过点P作PE⊥x轴于E,作PF⊥y轴于F,根据点P的坐标可得PE=PF=2,然后利用“HL”证明Rt△APE和Rt△BPF全等,根据全等三角形对应角相等可得∠APE=∠BPF,然后求出∠APB=∠EPF=90°,再根据垂直的定义证明;(2)求出AE的长度,再根据全等三角形对应边相等可得AE=BF,然后求出OB,再写出点B的坐标即可;(3)根据全等三角形对应边相等可得PE=PF,再表示出PE、PF,然后列出方程整理即可得解;(4)同(3)的思路求解即可.
试题解析:(1)如图1,过点P作PE⊥x轴于E,作PF⊥y轴于F
∵ P(2,2)
∴ PE=PF=2,∠EPF=90°
在Rt△APE和Rt△BPF中
![]()
∴ Rt△APE≌Rt△BPF(HL)
∴ ∠APE=∠BPF
∴ ∠APB=∠APE+∠BPE=∠BPF+∠BPE=90°
∴ PA⊥PB
(2)∵P(2,2)
∴ OE=OF=2
∵ A(8,0)
∴ OA=8
∴ AE=OA-OE=8-2=6
又由⑴得Rt△APE≌Rt△BPF
∴ BF=AE=6
∴ OB=BF-OF=6-2=4
∴ 点B的坐标为(0,-4)
(3)∵ Rt△APE≌Rt△BPF
∴ AE=BF
∵ AE=OA-OE=OA-2
BF=OF+OB= 2 +OB
∴ OA-2= 2 +OB
∴ OA -OB= 4
(4)OA +OB=4

 阅读快车系列答案
阅读快车系列答案