题目内容
【题目】如图，在△ABC中，∠ACB＝90°，点D，E在AB上，且AF垂直平分CD，BG垂直平分CE．(1)求∠ECD的度数；(2)若∠ACB为α，则∠ECD的度数能否用含α的式子来表示．
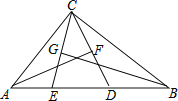
【答案】见解析
【解析】试题分析：
（1）由AF垂直平分CD可得AC=AD，再由等腰三角形的“三线合一”可得∠FAB=
∠CAB，同理可得∠GBA=
∠CBA；如图，设AF、BG相交于点O，则∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
（180°-∠ACB）=135°，由此在四边形GOFC中可得∠ECD=360°-∠CGO-∠CFO-∠GOF=360°-90°-90°-∠GOF=180°-135°=45°.
（2）思路同（1）只需把∠ACB=90°换成∠ACB= 
可解得∠DCE=90°- 
.
试题解析：
（1）如图，设AF、BG相交于点O，连接CO，
∵AF垂直平分CD，
∴AC=AD，∠CFO=90°，∴∠FAB=
∠CAB.
同理可得：∠CGO=90°，∠GBA=
∠CBA.
∴∠GOF=∠AOB=180°-∠FAB-∠GBA=180°-
（180°-∠ACB）=90°+
∠ACB=135°，
∵四边形GOFC的内角和为360°，
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-135°
=45°.
（2）同（1）可得∠GOF=90°+
∠ACB=90°+ 
，∠CFO=90°，∠CGO=90°，
∵四边形GOFC的内角和为360°，
∴∠ECD=360°-∠CGO-∠CFO-∠GOF
=360°-90°-90°-∠GOF
=180°-（90°+ 
）
=90°- 
.
【题目】为了提高学生书写汉字的能力，增强保护汉字的意识，我市举办了首届“汉字听写大赛”，经选拔后有50名学生参加决赛，这50名学生同时听写50个汉字，若每正确听写出一个汉字得1分，根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表：
组别 | 成绩x分 | 频数（人数） |
第1组 | 25≤x＜30 | 4 |
第2组 | 30≤x＜35 | 8 |
第3组 | 35≤x＜40 | 16 |
第4组 | 40≤x＜45 | a |
第5组 | 45≤x＜50 | 10 |
请结合图表完成下列各题：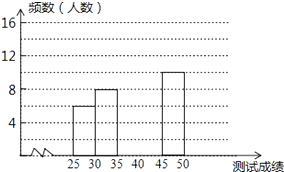
（1）求表中a的值；
（2）请把频数分布直方图补充完整；
（3）若测试成绩不低于40分为优秀，则本次测试的优秀率是多少？
