题目内容
【题目】如图,在△ABC中,AB=BC,AD⊥BC于点D,点E为AC中点且BE平分∠ABD,连接BE交AD于点F,且BF=AC,过点D作DG∥AB,交AC于点G.
求证:
(1)∠BAD=2∠DAC
(2)EF=EG.

【答案】见解析
【解析】试题分析:
(1)由AB=AC,E是AC的中点,可得BE⊥AC,∠DBA=2∠DBF;结合AD⊥BC可证得∠DBF=∠DAC,从而可证△BDF≌△ADC,得到AD=BD,
∴∠DAB=∠DBA=2∠DBF=2∠DAC;
(2)如图,延长BE、DG交于点K,①由DG∥AB和BE平分∠ABC可得∠K=∠DAK=∠DAC,从而可得DK=DB=DA;②由AB=BC,DG∥AB可得∠DGC=∠C,从而可得DG=DC=DF,由①②可得AD-DF=DK-DG,即AF=KG,最后通过证△AEF≌△KEG可得EF=EG.
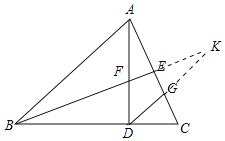
试题解析:
(1)∵AD⊥BC,∴∠ADC=∠BDF=90°,
∵AB=BC,E为AC的中点,
∴∠DBA=2∠CBE,BE⊥AC,
∴∠BEC=90°,
∴180°-∠C-∠ADC=180°-∠C-∠BEC,
即∠DBF=∠CAD,
在△BDF和△ADC中,
∠BDF=∠ADC=90°,∠DBF=∠CAD,BF=AC,
∴△BDF≌△ADC,
∴BD=AD,
∴∠BAD=∠ABD=2∠CBE=2∠DAC。
(2)延长BE、DG交于点k,

∵DG//AB,
∴∠CGD=∠CAB,∠k=∠ABE,
∵∠BAC=∠C,
∴∠CGD =∠C,
∵∠K=∠CBE=∠CAD,
∠AEF=∠KEG=90°,∠EAF=∠EKG,
∴DG=DC,DK=BD,
∴DG=DF,DK=BD=AD,
∴DK-DG=AD-DF,即GK=AF,
在Rt△AEF和Rt△KEG中,
∠AEF=∠KEG=90°,∠EAF=∠K,AF=GK,
∴Rt△AEF≌ Rt△KEG,
∴EF=EG.