题目内容
【题目】如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D是AC上一个动点,以AB为对角线的所有平行四边形ADBE中,线段DE的最小值是( )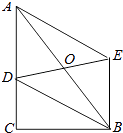
A.4
B.2 ![]()
C.2
D.6
【答案】A
【解析】解:∵在Rt△ABC中,∠B=90°,
∴BC⊥AC.
∵四边形ADBE是平行四边形,
∴OD=OE,OA=OB.
∴当OD取最小值时,DE线段最短,此时OD⊥BC.
∴OD∥CB.
又点O是AB的中点,
∴OD是△ABC的中位线,
∴OD= ![]() CB=2,
CB=2,
∴ED=2OD=4.
所以答案是:A.
【考点精析】本题主要考查了垂线段最短和三角形中位线定理的相关知识点,需要掌握连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半才能正确解答此题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目