题目内容
【题目】如图,把长方形纸片ABCD沿EF折叠后,使得点D落在点H的位置上,点C恰好落在边AD上的点G处,连接EG.
(1)△GEF是等腰三角形吗?请说明理由;
(2)若CD=4,GD=8,求HF的长度.
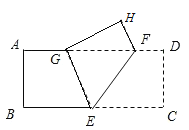
【答案】(1)见解析(2)3.
【解析】
(1)由翻折的性质得∠FEC=∠GEF,由长方形纸片的上下两边平行,可得∠GFE=∠FEC,所以∠GFE=∠GEF,根据“等角对等边”可知△GEF是等腰三角形;
(2)由翻折的性质可知GH=DC=4,HF=DF,设HF长为x,则GF长为(8-x),由勾股定理可得x2+42=(8-x)2,从而得到x=3,然后根据HF=DF,可求得HF=3.
(1)∵长方形纸片ABCD,
∴AD∥BC,
∴∠GFE=∠FEC,
∵∠FEC=∠GEF,
∴∠GFE=∠GEF,
∴△GEF是等腰三角形.
(2)∵∠C=∠F=90°,HF=DF,GD=8,
设HF长为x,则GF长为(8-x),
在RT△ABD中,x2+42=(8-x)2,解得x=3,
∴HF的长为3.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某件商品的成本价为15元,据市场调查得知,每天的销量y(件)与价格x(元)有下列关系:
销售价格x | 20 | 25 | 30 | 50 |
销售量y | 15 | 12 | 10 | 6 |
(1)根据表中数据,在直角坐标系中描出实数对(x,y)的对应点,并画出图象;
(2)猜测确定y与x间的关系式;
(3)设总利润为W元,试求出W与x之间的函数关系式,若售价不超过30元,求出当日的销售单价定为多少时,才能获得最大利润?
【题目】声音在空气中传播的速度y(m/s)(简称音速)与气温x(℃)的关系如下表:
气温x(℃) | 0 | 5 | 10 | 15 | 20 |
音速y(m/s) | 331 | 334 | 337 | 340 | 343 |
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速y(m/s)与气温x(℃)之间的关系式;
(3)气温x=22℃时,某人看到烟花烯放5s后才听到声音,那么此人与燃烟花的所在地约相距多远?