题目内容
【题目】如图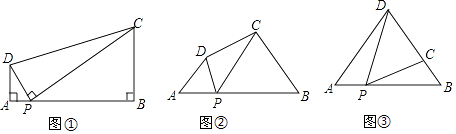
(1)问题:如图①,在四边形ABCD中,点P为AB上一点,∠DPC=∠A=∠B=90°.
求证:ADBC=APBP.
(2)探究:如图②,在四边形ABCD中,点P为AB上一点,当∠DPC=∠A=∠B=θ,上述结论是否依然成立?说明理由.
(3)应用:请利用(1)(2)获得的经验解决问题:
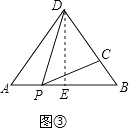
如图③,在△ABD中,AB=6,AD=BD=5,点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠DPC=∠A,设点P的运动时间为t秒,当以D为圆心,以DC为半径的圆与AB相切时,求t的值.
【答案】
(1)证明:∵∠DPA+∠CPB=90°,∠DPA+∠ADP=90°,
∴∠PDA=∠CPB,
又∵∠A=∠B=90°,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(2)解:结论:ADBC=APBP仍然成立,
理由:∵∠ADP+∠APD=180°﹣θ,∠DPA+∠CPB=180°﹣θ,
∴∠ADP=∠CPB,
又∵∠A=∠B=θ,
∴△ADP∽△BPC,
∴ ![]() =
=![]() ,
,
∴AD·BC=AP·BP.
(3)解:作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,
∴DE=![]() =4,
=4,
∴DC=4,
∴BC=1,
依据(1)(2)的结论AD·BC=AP·BP,
∴5×1=t(6﹣t),
∴t2﹣6t+5=0,
解得:t1=1,t2=5,
∴点P运动时间为1s或5s.
【解析】(1)由同角的余角相等得∠PDA=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]()
![]()
![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(2)结论:AD·BC=AP·BP仍然成立;理由:由等量代换得∠ADP=∠CPB,根据相似三角形的判定得△ADP∽△BPC,再由相似三角形的性质得出![]() =
=![]() ,即AD·BC=AP·BP.
,即AD·BC=AP·BP.
(3)作DE⊥AB,当⊙D与AB相切时,半径r=DE=DC,由勾股定理得DE=DC=4,依据(1)(2)的结论AD·BC=AP·BP,即t2﹣6t+5=0,解之即可得出答案.

 精英口算卡系列答案
精英口算卡系列答案【题目】某校兴趣小组对网上吐糟较为频繁的“医患关系”产生了兴趣,利用节假日在某社区开展了“造成医患关系紧张的原因”的问卷调查.
造成医患关系紧张的原因(单选) |
根据调查结果绘制出了如下两幅尚不完整的统计图.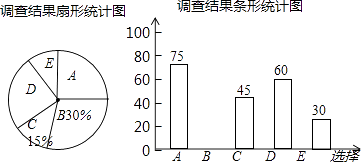
根据以上信息解答下列问题:
(1)这次接受调查的总人数为人;
(2)在扇形统计图中,“A”所在扇形的圆心角的度数为;
(3)补全条形统计图;
(4)若该市有1000万人,请你估计选D的总人数.