题目内容
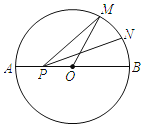
【题目】如图,AB是圆O的直径,AB=8,点M在圆O上,∠MOB=60°,N是![]() 的中点,P为AB上一动点,则PM+PN的最小值是_____.
的中点,P为AB上一动点,则PM+PN的最小值是_____.
【答案】4![]() .
.
【解析】
作点M关于AB的对称点M',连接NM',交AB于点P,此时PM+PN有最小值,连接ON,OM,利用垂径定理,求出∠M'OB=∠MOB=60°,进一步求出∠NOM'=90°,在等腰直角三角形NOM'中求出NM'的长度即可.
解:如图,作点M关于AB的对称点M',连接NM',交AB于点P,此时PM+PN有最小值,
连接ON,OM,
则OB垂直平分MM',![]() ,
,
∴∠M'OB=∠MOB=60°,
∵N是![]() 的中点,
的中点,
∴![]() ,
,
∴∠MON=∠BON=![]() ∠MOB=30°,
∠MOB=30°,
∴∠NOM'=∠NOB+∠M'OB=90°,
∵AB=8,
∴ON=OM'=4,
在等腰Rt△ONM'中,
NM'=![]() ON=4
ON=4![]() ,
,
∵MP=M'P,
∴MP+NP=M'N=4![]() ,
,
故答案为:4![]() .
.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目