题目内容
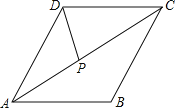
【题目】如图，菱形ABCD的边长为4，∠B＝120°．点P是对角线AC上一点（不与端点A重合），则线段
AP+PD的最小值为_____．
【答案】2
【解析】
作PE⊥AB于点E，DF⊥AB于点F，由菱形的性质可得∠DAC=∠CAB，AB=BC，由等腰三角形的性质和直角三角形的性质可得PE=
AP，AF=AD=2，DF=AF=2，可得AP+PD=PE+DP，则点D，点P，点E三点共线且垂直AB时，PE+DP的值最小，即可求线段AP+PD的最小值．
解：如图，作PE⊥AB于点E，DF⊥AB于点F，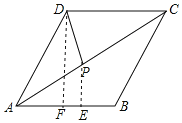
∵四边形ABCD是菱形
∴∠DAC=∠CAB，AB=BC，且∠B=120°
∴∠CAB=30°
∴PE=AP，∠DAF=60°
∴∠FDA=30°，且DF⊥AB
∴AF=AD=2，DF=AF=2
∵AP+PD=PE+DP
∴当点D，点P，点E三点共线且垂直AB时，PE+DP的值最小，最小值为DF，
∴线段AP+PD的最小值为2
故答案为：2
练习册系列答案
相关题目
