��Ŀ����
����Ŀ����һԪ���η����У���������Τ�ﶨ��������һԪ���η���ax2+bx+c��0��a��0�����������������ʵ����x1��x2����ôx1+x2����![]() ��x1x2��
��x1x2��![]() ��˵����������������������0�������緽��2x2��3x��1��0�У�����17�����Ը÷������������ȵ�ʵ���⣮�Ƿ��̵�����Ϊx1��x2����ôx1+x2��
��˵����������������������0�������緽��2x2��3x��1��0�У�����17�����Ը÷������������ȵ�ʵ���⣮�Ƿ��̵�����Ϊx1��x2����ôx1+x2��![]() ��x1x2����
��x1x2����![]() ��������Ķ����Ͻ�����и��⣺
��������Ķ����Ͻ�����и��⣺
��1����֪����x2��3x��2��0������Ϊx1��x2����x1��x2�������и�ʽ��ֵ��
��x12+x22����![]() ��
��
��2����֪x1��x2��һԪ���η���4kx2��4kx+k+1��0������ʵ������
���Ƿ����ʵ��k��ʹ��2x1��x2����x1��2x2������![]() �����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
�����������ڣ����k��ֵ���������ڣ���˵�����ɣ�
����ʹ![]() ��ֵΪ������ʵ��k������ֵ��
��ֵΪ������ʵ��k������ֵ��
���𰸡�(1) ��x12+x22��13, ��![]() ;(2) �ٲ�����,���ɼ���������k����2��3��5
;(2) �ٲ�����,���ɼ���������k����2��3��5
��������
��1����Τ�ﶨ��д��x1+x2��x1x2��ֵ���ѣ�x1+x2��2������ȫƽ����ʽ������â٣�ͨ����ֵ��âڣ�
��2�����������0ʱ��k��ȡֵ��Χ����Τ�ﶨ��д����k��ʾx1+x2��x1x2��ֵ����ֱ�Ӱѵ�ʽ���չ�����Σ�����x1+x2��x1x2��ʽ�ӣ������k���ڻ���ʽ�ӵõ�k�ڷ�ĸ�ķ�ʽ������ʽ�ӵ�ֵΪ������k��ȡֵ��Χȷ��k��ֵ��
��1����x2��3x��2��0��b2��4ac������3��2��4������2����17��0��
��x1+x2��3��x1x2����2��
��x12+x22����x1+x2��2��2x1x2��32��2������2����9+4��13��
��![]() ��
��
��2���߷���������ʵ������
��b2��4ac������4k��2��44k��k+1����0��
��k��0��x1+x2��1��x1x2��![]() ��
��
�١ߣ�2x1��x2����x1��2x2����2x12��5x1x2+2x22��2��x12+2x1x2+x22����9x1x2��2��x1+x2��2��9x1x2��
��![]() ��
��
��ã�k��![]() ����k��0ì�ܣ�
����k��0ì�ܣ�
�����k��ֵ��ʹ��2x1��x2����x1��2x2������![]() ������
������
��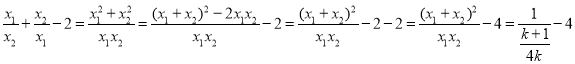
![]() ��
��
��![]() ��ֵΪ������
��ֵΪ������
��k+1����1����2����4��
�֡�k��0��
��k����2��3��5.

����Ŀ��ij��ͬѧΪ�˽�2019��ijС����ͥ�¾���ˮ�������������˸�С�����ּ�ͥ�������������ݽ����������£�
�¾���ˮ��x��t�� | Ƶ�������� | Ƶ�� |
| 6 | 0.12 |
| 0.24 | |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | |
| 2 | 0.04 |

�����������⣺
��1���������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
��2�����С����ˮ��������15t�ļ�ͥռ�������ͥ�����İٷֱȣ�
��3������С����1000����ͥ�����ݵ������ݹ��ƣ���С���¾���ˮ������20t�ļ�ͥ��Լ�ж��ٻ���