题目内容
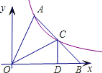
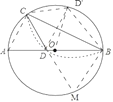
【题目】如图,在⊙O中,将![]() 沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
沿弦BC所在直线折叠,折叠后的弧与直径AB相交于点D,连接CD.
(1)若点D恰好与点O重合,则∠ABC= °;
(2)延长CD交⊙O于点M,连接BM.猜想∠ABC与∠ABM的数量关系,并说明理由.

【答案】(1) 30;(2) ∠ABM=2∠ABC,理由见解析.
【解析】
(1)根据折叠的性质和圆周角定理解答即可;
(2)作点D关于BC的对称点D',利用对称的性质和圆周角定理解答即可.
(1)∵由折叠可知:∠OBC=∠CBD,
∵点D恰好与点O重合,
∴∠COD=60°,
∴∠ABC=∠OBC=![]() ;
;
故答案为:30;
(2)∠ABM=2∠ABC,理由如下:
作点D关于BC的对称点D',连接CD',BD',
由对称可得∠DBC=∠D'BC,DC=D'C,
连接CO,D'O,AC,
∴∠AOC=2∠ABC,∠D'OC=2∠D'BC,
∴∠AOC=∠D'OC,
∴AC=D'C,
∵DC=D'C,
∴AC=DC,
∴∠CAD=∠CDA,
∵AB是直径,
∴∠ACB=90°,
∴∠CAD+∠ABC=90°,
设∠ABC=α,则∠CAD=∠CDA=90°﹣α,
∴∠ACD=180°﹣∠CAD﹣∠CDA=2α,
即∠ACD=2∠ABC,
∵∠ABM=∠ACD,
∴∠ABM=2∠ABC.

练习册系列答案
相关题目