题目内容
如图,在梯形ABCD中,AD∥BC,AB=AD+BC,E为CD的中点.
求证:AE⊥BE.
求证:AE⊥BE.

略
取AB的中点F,并连接EF,可以得到EF为梯形的中位线,利用梯形的中位线定理即可证得结论.
证明:取AB的中点F,并连接EF(3分)
∵AD∥BC,
∴EF= (AD+CB)
(AD+CB)
∵AB=AD+BC
∴EF= AB
AB
∴△ABE直角三角形,AB是斜边,
∴AE⊥BE.
证明:取AB的中点F,并连接EF(3分)
∵AD∥BC,
∴EF=
 (AD+CB)
(AD+CB)∵AB=AD+BC
∴EF=
 AB
AB∴△ABE直角三角形,AB是斜边,
∴AE⊥BE.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目

 ,则
,则 的度数是
的度数是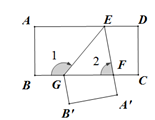
 中,点
中,点 是
是 的中点,连接
的中点,连接 、
、 ,点
,点 是
是 、
、 ,点
,点 是
是 ,过点
,过点 于点
于点 ,连接
,连接 .下列结论中
.下列结论中 ;②
;② ;③
;③ ;④
;④



