题目内容
如图①,在等腰梯形ABCD中,AD∥BC,AB=CD,上底AD=2,梯形的高也等于2。一动点P从C出发,沿CB方向在线段BC上作匀速运动。
(1)若三角形ABP的面积S关于运动时间t的函数图象如图②所示,则可得BC长为 ; ;(4分。)
(2)在(1)的条件下,试求∠B的度数。(4分。)


图① 图②
(1)若三角形ABP的面积S关于运动时间t的函数图象如图②所示,则可得BC长为 ; ;(4分。)
(2)在(1)的条件下,试求∠B的度数。(4分。)


图① 图②
(1) BC=6 (2) ∠B=45°
分析:
(1)利用设P点的运动速度为v,则PC=vt,BP=BC-PC,即可得出BC-2v=3,进而求出即可;
(2)利用全等三角形的判定得出△ABE≌△DCF,进而得出四边形AEFD是正方形,进而得出答案。
解答:
(1)设P点的运动速度为v,则PC=vt,BP=BC-PC,
∵当t=2时,s=3,
∴1/2(BC-PC)?2=3,
BC-2v=3,①
∵当t=4时,s=0,
∴1/2(BC-PC)?2=0,
CB-4v=0,②
①-②得:2v=3,
v=1.5,
∴BC=4×1.5=6;
(2)如图①,过A作AE⊥CB,过D作DF⊥BC,

∴∠BEA=∠CFD=90°,
∵梯形ABCD是等腰梯形,
∴AB=CD,∠B=∠C,
∴△ABE≌△DCF,
∴BE=CF,
∵上底AD=2,梯形的高也等于2,
∴四边形AEFD是正方形,
∴AD=EF=2,
∵CB=6,
∴BE=FC=2,
∴∠B=45°。
点评:此题主要考查了等腰梯形的性质以及全等三角形的判定,根据常用辅助线得出BE=FC进而得出是解题关键。

练习册系列答案
相关题目





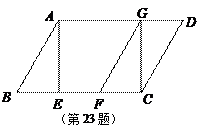
 =
= ,
, =
= ,
, =
= 。问:
。问:
