题目内容
如图,平面直角坐标系中,抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),与y轴交于点C,抛物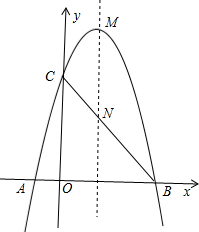 线的顶点为点M,对称轴与线段BC交于点N,点P为线段BC上一个动点(与B、C不重合).
线的顶点为点M,对称轴与线段BC交于点N,点P为线段BC上一个动点(与B、C不重合).(1)求点A、B的坐标;
(2)在抛物线的对称轴上找一点D,使|DC-DB|的值最大,求点D的坐标;
(3)过点P作PQ∥y轴与抛物线交于点Q,连接QM,当四边形PQMN满足有一组对边相等时,求P点的坐标.
分析:(1)根据二次函数与图象的交点坐标求法,y=0,求出x即可;
(2)利用轴对称图形的性质可以得出D点坐标的位置,利用D点在直线AC解析式上,即可求出;
(3)利用平行四边形的性质以及等腰梯形性质分别求出即可.
(2)利用轴对称图形的性质可以得出D点坐标的位置,利用D点在直线AC解析式上,即可求出;
(3)利用平行四边形的性质以及等腰梯形性质分别求出即可.
解答: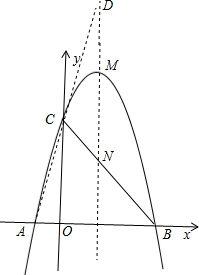 解:(1)∵抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),
解:(1)∵抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),
∴抛物线与x轴的交点坐标为:0=-x2+3x+4,
解得:x1=-1,x2=4,
A(-1,0)、B(4,0);
(2)连接AC并延长交抛物线的对称轴于D,
将A(-1,0),C(0,4)点的坐标代入:Y=kx+b,
解得:b=4,k=4,
求出直线AC解析式:y=4x+4,
将x=1.5,代入y=4x+4得,
y=10,
∴D点坐标(1.5,10)
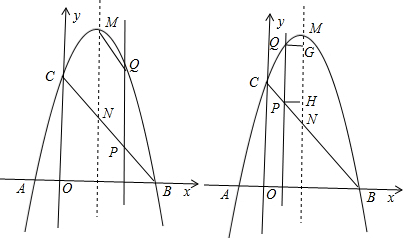
(3)设P(x,-x+4),Q(x,-x2+3x+4),
①四边形PQMN是平行四边形,此时PQ=MN,
由题意得,
-
=(-x2+3x+4)-(-x+4)
解得:x=2.5,x=1.5(舍去)
此时P(2.5,1.5),
②四边形PQMN是等腰梯形,此时PN=QM进一步得MG=NH(QG、PH是所添的垂线段),
从而得方
+x2-3x-4=-x+4-
,
解得x=0.5,x=1.5(舍去),
此时P(0.5,3.5),
综合上述两种情况可知:当四边形PQMN满足有一组对边相等时,
P点的坐标为(2.5,1.5)或(0.5,3.5).
 解:(1)∵抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),
解:(1)∵抛物线y=-x2+3x+4与x轴交于点A、B(A在左侧),∴抛物线与x轴的交点坐标为:0=-x2+3x+4,
解得:x1=-1,x2=4,
A(-1,0)、B(4,0);
(2)连接AC并延长交抛物线的对称轴于D,
将A(-1,0),C(0,4)点的坐标代入:Y=kx+b,
|
解得:b=4,k=4,
求出直线AC解析式:y=4x+4,
将x=1.5,代入y=4x+4得,
y=10,
∴D点坐标(1.5,10)

(3)设P(x,-x+4),Q(x,-x2+3x+4),
①四边形PQMN是平行四边形,此时PQ=MN,
由题意得,
| 25 |
| 4 |
| 5 |
| 2 |
解得:x=2.5,x=1.5(舍去)
此时P(2.5,1.5),
②四边形PQMN是等腰梯形,此时PN=QM进一步得MG=NH(QG、PH是所添的垂线段),
从而得方
| 25 |
| 4 |
| 5 |
| 2 |
解得x=0.5,x=1.5(舍去),
此时P(0.5,3.5),
综合上述两种情况可知:当四边形PQMN满足有一组对边相等时,
P点的坐标为(2.5,1.5)或(0.5,3.5).
点评:此题主要考查了二次函数与一次函数的综合应用以及平行四边形与梯形的性质等知识,二次函数的综合应用是初中阶段的难点问题,同学们在解答的过程中特别注意解题的技巧性从而降低计算量.

练习册系列答案
相关题目
 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.