题目内容
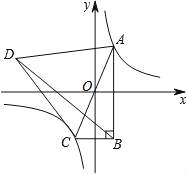
【题目】如图,已知双曲线y=![]() (k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20
(k≠0)与正比例函数y=mx(m≠0)交于A、C两点,以AC为边作等边三角形ACD,且S△ACD=20![]() ,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
,再以AC为斜边作直角三角形ABC,使AB∥y轴,连接BD.若△ABD的周长比△BCD的周长多4,则k的值是_______.
【答案】8
【解析】如图所示:记AB与x轴的交点为E.
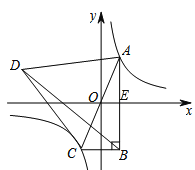
∵以AC为边作等边三角形ACD,且S△ACD=![]() ,
,
∴设AC的长为x,则AC边上的高为:![]() ,
,
∴![]() ,解得:
,解得:![]() (负数舍去),即
(负数舍去),即![]() ,
,
∵△ABD的周长比△BCD的周长多4,AD=DC,BD是公共边,
∴AB-BC=4.
设BC=y,则AB=4+y,故![]() ,解得:y1=4,y2=-8(不合题意舍去),
,解得:y1=4,y2=-8(不合题意舍去),
∴BC=4,AB=8.
由反比例函数的性质可得:AO=CO,
∵OE∥BC,
∴OE是△ABC的中位线,
∴EO=2,AE=4,
∴k=2×4=8.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目