题目内容
【题目】如图，在Rt△ABC中，∠C=90°，AC=BC，AB=8，点D为AB的中点，若直角MDN绕点D旋转，分别交AC于点E，交BC于点F，则下列说法正确的有（ ） ①AE=CF；②EC+CF=4 
；③DE=DF；④若△ECF的面积为一个定值，则EF的长也是一个定值．
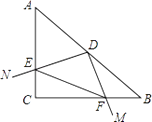
A.①②
B.①③
C.①②③
D.①②③④
【答案】D
【解析】解：①连接CD．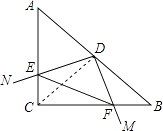 
∵在Rt△ABC中，∠C=90°，AC=BC，点D为AB的中点，
∴CD⊥AB，CD=AD=DB，
在△ADE与△CDF中，∠A=DCF=45°，AD=CD，∠ADE=∠CDF，
∴△ADE≌△CDF，
∴AE=CF．说法正确；
②∵在Rt△ABC中，∠C=90°，AC=BC，AB=8，
∴AC=BC=4 
．
由①知AE=CF，
∴EC+CF=EC+AE=AC=4 ．说法正确；
③由①知△ADE≌△CDF，
∴DE=DF．说法正确；
④∵△ECF的面积= 
×CE×CF，如果这是一个定值，则CECF是一个定值，
又∵EC+CF=4 ，
∴可唯一确定EC与EF的值，
再由勾股定理知EF的长也是一个定值，说法正确．
故选D．
【考点精析】认真审题，首先需要了解全等三角形的性质(全等三角形的对应边相等; 全等三角形的对应角相等)，还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键．
练习册系列答案
相关题目
