题目内容
如图,A、B是太湖中的两个景点,C为湖中另一个景点.景点C在景点B的正西方向,从景点A看,景点C在北偏东30°方向,景点B在北偏东75°方向.一游客自景点A驾船以每分钟20米的速度行驶了16分钟到达景点C,之后又以同样的速度驶向景点B,该游客从景点C到景点B需用多长时间?(精确到1分钟)
(参考数据: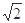 ≈1.41、
≈1.41、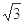 ≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
(参考数据:
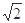 ≈1.41、
≈1.41、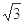 ≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
≈1.73、 sin75°≈0.97、cos75°≈0.26、tan75°≈3.73)
44
由各方向角可得△ABC的各内角,可先由AC求出AD及CD的长,再在Rt△ABC中求出BD的长,则BC的长也可得出,再求得游客从景点C到景点B需用的时间即可.
延长BC交点A的正北方向所在直线于点D.
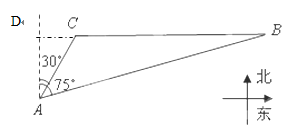
据题意得AD⊥BD,AC=16×20=320m. 1分
在Rt△ADC中∠DAC=30°,AC=320m
可得:AD=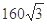 m,
m,
DC=160m 3分
在Rt△ADB中∠DAB=75°,AD=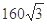 m
m
tan∠DAB=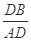
∴tan75°=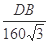 ,
,
DB=tan75°×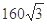 5分
5分
≈3.73×160×1.73≈1032.46 m 6分
而BC=BD-CD≈1032.46-160=872.46 m
∴872.46÷20=43.623≈44
延长BC交点A的正北方向所在直线于点D.

据题意得AD⊥BD,AC=16×20=320m. 1分
在Rt△ADC中∠DAC=30°,AC=320m
可得:AD=
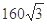 m,
m, DC=160m 3分
在Rt△ADB中∠DAB=75°,AD=
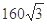 m
mtan∠DAB=
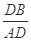
∴tan75°=
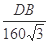 ,
, DB=tan75°×
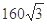 5分
5分≈3.73×160×1.73≈1032.46 m 6分
而BC=BD-CD≈1032.46-160=872.46 m
∴872.46÷20=43.623≈44

练习册系列答案
相关题目
 )米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).
)米,又知在A处观测山顶P的仰角为45°,求AB两地的距离及小山的高(结果保留根号).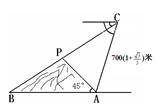

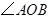 如右图放置,则sin∠AOB的值为( ▲ )
如右图放置,则sin∠AOB的值为( ▲ )
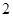
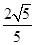
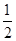
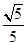
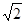 ≈1.414,
≈1.414,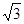 ≈1.732)
≈1.732)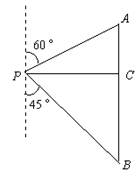
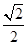 │+(
│+(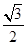 -cosB)=0,则∠C=____度.
-cosB)=0,则∠C=____度.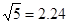 ,
,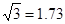 ,
, ,结果保留两个有效数字).
,结果保留两个有效数字).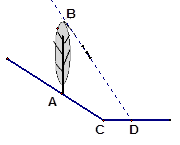
 .
.